Parabola con squadra e compasso
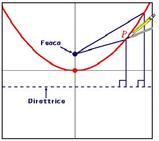
Disegniamo un sistema di assi coordinati ortogonali. Poi tanti cerchi con centro sull'asse verticale e tangenti in un medesimo punto come mostra la figura.
Dai punti d'intersezione dei cerchi con l'asse orizzontale solleviamo delle perpendicolari. Per ciascun cerchio poi tracciamo una tangente parallela all'asse orizzontale fino ad incontrare le verticali appena tracciate. I punti d'intersezione sono punti appartenenti alla parabola.
Infatti il segmento di colore rosso lo assumiamo come segmento unitario, inoltre quello viola sia di lunghezza a e quello verde di lunghezza x (da calcolare).
Allora si ha 
.
Osservazione: non sembrerebbe che x = a2 perchè ad occhio il segmento di lunghezza x è più corto del segmento di lunghezza a; ma non dimentichiamo che il segmento rosso è assunto come unitario ed è più lungo di quello viola quindi a
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
