Definizioni fondamentali della geometria

In quest'appunto troverai le principali definizioni relative al mondo della geometria, raggruppate per ente di riferimento.

La definizione di assioma e teorema

La matematica è fatta di teoremi e assiomi. Gli assiomi sono delle proprietà che non hanno bisogno di essere dimostrate.

Un teorema, invece, è una proposizione che si deduce da un insieme di assiomi, formato da ipotesi e tesi.

La dimostrazione è l’insieme dei passaggi logici che dall’ipotesi conduce alla tesi. E' un'assioma quello di appartenenza, il quale afferma che esistono infiniti sottoinsiemi propri del piano ossia le rette, tali che per ogni coppia di punti distinti esiste una e una sola retta che li contiene. Inoltre, anche l'assioma dell'ordine è fondamentale: esso afferma che ogni retta è dotata di due versi naturali, uno opposto all’altro, rispetto ai quali è aperta, densa e illimitata.

Quando si parla di piani, bisogna citare un terzo assioma, il quale prende il nome di assioma del piano. Esso sancisce che una retta divide il piano a cui appartiene in due regioni di punti che godono delle seguenti proprietà:

• se due punti appartengono a una stessa regione, allora il segmento che li congiunge non interseca la retta
• se due punti appartengono a regioni diverse, allora il segmento che li congiunge interseca la retta

La differenza tra semirette, segmenti consecutivi e segmenti adiacenti

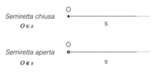
Un'altra differenza fondamentale da conoscere quando si parla di geometria è quella che intercorre tra semirette e segmenti.
Una semiretta è una parte di retta delineata da un punto di origine. Ogni retta è suddivisa dall’origine in due semirette opposte. D'altro canto, un segmento è una parte di retta delimitata da due punti detti estremi. A differenza delle prime, quindi, i segmenti hanno un'origine e una fine. Se questi ultimi due punti coincidono, il segmento si definisce segmento nullo.

Due o più segmenti presenti sullo stesso piano possono essere classificati a seconda della posizione reciproca. In particolare, essi sono distinguibili in:

• segmenti consecutivi, ossia segmenti che hanno un estremo in comune. Se essi non sono sovrapposti e hanno in comune un solo estremo, l'insieme dei segmenti prende il nome di poligonale
• segmenti adiacenti, cioè segmenti consecutiviche appartengono l’uno al prolungamento dell’altro

Come definire un angolo e come classificarli a seconda dell'ampiezza

Le semirette possono delimitare un angolo, mentre un insieme di segmenti consecutivi e chiusi possono definire una figura. Quest'ultima può essere convessa se contiene il segmento che congiunge due punti qualsiasi al suo interno. Si dice concava se non lo contiene.

Ritornando agli angoli, anch'essi possono essere convessi. In particolare, si dice convesso quando non contiene i prolungamenti dei lati e si dice concavo quando li contiene. Un singolo angolo può essere classificato a seconda dell'ampiezza in:

• angolo giro (
  [math]360°[/math]
  ), cioè un angolo i cui lati sono semirette coincidenti e che comprende tutti i punti del piano
• angolo piatto (
  [math]180°[/math]
  ), ossia un angolo i cui lati sono semirette opposte
• angolo nullo (
  [math]0°[/math]
  ), cioè un angolo i cui lati sono semirette coincidenti e che non ha alcun punto interno
• angolo acuto, se l'ampiezza è minore di
  [math]90°[/math]
• angolo ottuso, se l'ampiezza è maggiore di
  [math]90°[/math]
• angolo retto, se l'ampiezza è pari a
  [math]90°[/math]

Se, invece, sono presenti più angoli su uno stesso piano, questi possono essere distinti tra:

• angoli adiacenti: sono adiacenti gli angoli che hanno un lato in comune e gli altri due lati sulla stessa retta, da parti opposte. Due angoli adiacenti sono anche supplementari
• angoli consecutivi: due angoli che hanno il vertice e un lato in comune e gli altri due lati da parti opposte rispetto al lato comune
• angoli opposti al vertice: due angoli che hanno lo stesso vertice e i lati dell’uno sono il prolungamento dei lati dell’altro
• angoli esplementari: due angoli consecutivi che hanno in comune anche il secondo lato e la loro somma forma un angolo giro
• angoli complementari: due angoli la cui somma è un angolo retto.

Secondo alcuni teoremi, alcuni di questi angoli godono di proprietà particolari. Più precisamente angoli supplementari ad angoli congruenti sono angoli congruenti. Angoli opposti al vertice sono congruenti. La metà di angoli congruenti sono congruenti.

Per ulteriori approfondimenti sui concetti fondamentali della geometria vedi anche qua