Finale al Grande Slam

Roland Garros è un torneo di tennis che fa parte del gruppo Grande Slam. Si tiene a Parigi a cavallo tra maggio e giugno. Gli incontri delle diverse gare sono ormai terminati. E' in corso la finale di singolare maschile. A pomeriggio inoltrato i due campioni Rafael Nadal e Roger Federer, ancora una volta sfidanti in finale, sono prossimi a concludere il torneo sul prestigioso campo in terra battuta. Dopo una serie di scambi velocissimi da fondo campo, Federer intravvede la possibilità di chiudere il game con un furbo cross da sottorete.

Ma Rafa, con un allungo prodigioso riesce a intercettare la palla e decide di segnare il punto con un poderoso tiro mancino (per lui è il diritto) in lungolinea, come da disegno.

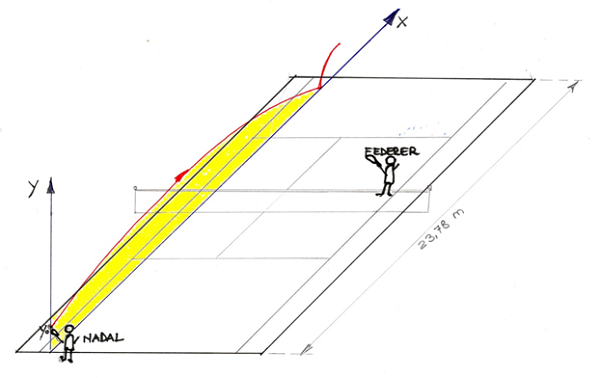
Domanda 1. Scrivere le equazioni del moto della palla lanciata da Nadal, per i seguenti due modelli:
(1) moto trascurando l'attrito dell'aria (caso ideale)
(2) moto tenendo conto dell'attrito dell'aria (caso reale).

Per risolvere il caso reale si tenga presente che l'attrito dell'aria si manifesta per il tramite della resistenza aerodinamica, esprimibile come:

.

Questa forza si oppone al moto ed è diretta in senso inverso rispetto al vettore velocità.

Domanda 2.Assumendo che la pallina, nell'istante iniziale in cui viene colpita dalla racchetta di Nadal parta con velocità v0 pari a 120 km/h e con un angolo α= 3,5° rispetto all'asse orizzontale x, determinare per i due casi ( di Domanda 1) se la palla batte in campo avversario oppure se va oltre la linea di fondo.

Date le dimensioni del campo da tennis (disegno allegato) Usare i seguenti dati:
C = coef. di resistenza (0.5 per la sfera in moto turbolento come in questo caso)
ρ = densità aria (1,205 kg/m^3)
d = diametro palla (6 cm)
m = massa palla(58 g)
yo = altezza palla (1.60 m) all'istante iniziale
S = sezione trasversa della palla da tennis (m^2)
v = modulo del vettore velocità (m/s)

Verificare anche che la palla non finisca in rete, essendo distanza (Nadal-rete) pari a 11.89 m, e altezza rete = 1 m.

Traccia per la soluzione: risolvere le equazioni del moto scritte per rispondere alla Domanda 1 (2° principio della dinamica) lungo gli assi x (parallelo al campo da gioco) e y (perpendicolare).

Per entrambi i casi le equazioni per gli assi x e y sono disaccoppiate e qundi si possono risolvere separatamente.

Mentre nel caso (1) è immediato trovare le soluzioni analitiche, nel caso (2) la ricerca della soluzione alle quadrature è complessa e molto laboriosa ed è quindi più agevole risolvere con metodi numerici, ad es. Runge-Kutta.

Questo problema vuole essere un omaggio ai due campioni, per i quali l'autore non nasconde il suo entusiasmo.

Soluzione del problema
File di Excel