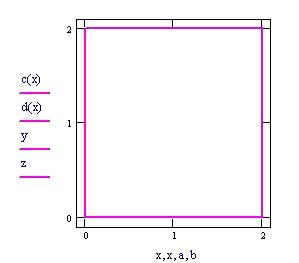
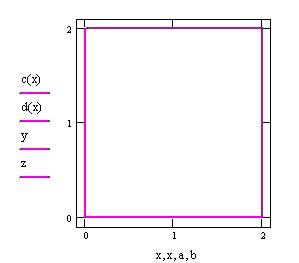
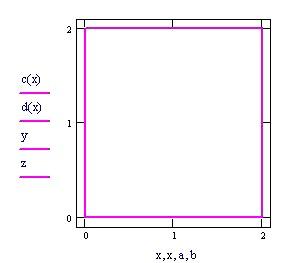
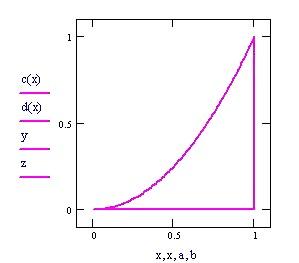
Definiamo la frontiera della regione del piano x-y :
A ssumiamo e per ogni x .
I ntegrali Doppi variabili calcolati numericamente ( Carlo Elce )
Partendo da una funzione, che rappresenta un piano variabile parallelo al piano x-y su cui è definito un dominio quadrato, viene evidenziato come un integrale doppio calcoli il volume di un parallelepipedo. Facendo poi variare la funzione e il dominio piano viene mostrato come l'integrale doppio calcoli il volume di un solido delimitato da una superficie più generale .
.
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
Definiamo una nuova funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
Definiamo una terza funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
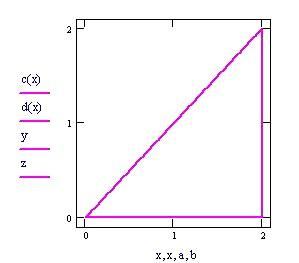
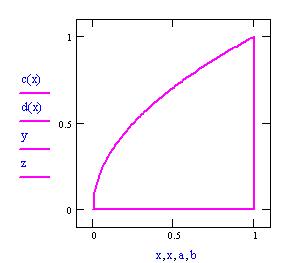
Definiamo una nuova frontiera della regione del piano x-y :
assumiamo e
per ogni x .
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
Definiamo una nuova frontiera della regione del piano x-y :
assumiamo e
per ogni x .
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
Definiamo una nuova frontiera della regione del piano n x-y :
assumiamo e
per ogni x.
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
Contenuto originale e autentico, validato dal Team di Esperti di Skuola.net



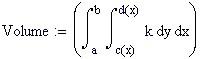
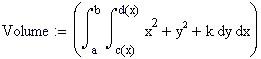
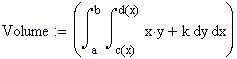
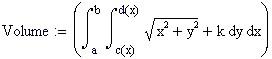
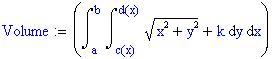
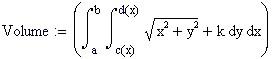
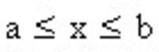





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo