[math]2x+3-|x+1|=|3x+1|[/math]
[math]2x+3-|x+1|=|3x+1|[/math]
;Studiamo il segno di ciascun argomento dei moduli e costruiamo la tabella
nella quale riportare la loro variazione:
[math]x+1>=0 => x>=-1[/math]
[math]3x+1>=0 => x>=-1/3[/math]
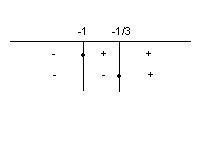
Distinguiamo adesso i seguenti casi:
1)Per
[math]x>-1[/math]
, entrambi gli argomenti sono negativi
[math]2x+3-|x+1|=|3x+1|[/math]
;è equivalente all'equazione
[math]2x+3+x+1=-3x-1[/math]
;Semplificando
[math]6x=-5 => x=-5/6[/math]
.La soluzione non è accettabile per la condizione
[math]x>-1[/math]
. 2)Per
[math]-1>=x>=-1/3[/math]
l'argomento del primo modulo è postivo e quello del secondo è negativo
[math]2x+3-|x+1|=|3x+1|[/math]
;[math]2x+3-x-1=-3x-1[/math]
;Semplificando
[math]4x=-3 => x=-3/4[/math]
. La soluzione è accettabile per la condizione
[math]-1>=x>=-1/3[/math]
. 3)Per
[math]x> -1/3[/math]
, entrambi gli argomenti sono positivi
[math]2x+3-|x+1|=|3x+1|[/math]
;[math]2x+3-x-1=3x+1[/math]
;[math]-2x=-1 => x=1/2[/math]
.Soluzione accettabile per la condizione
[math]x> -1/3[/math]
. Pertanto la soluzione dell'equazione di partenza sarà
[math]S={1/2; -3/4}[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
