Matemilano, percorsi matematici in città

Ominide

5 min. di lettura

Vota

Concetti Chiave

Il libro "Matemilano" è una raccolta di saggi che esplorano le applicazioni della matematica nella vita quotidiana, ispirato dalla mostra ideata dal Dipartimento di Matematica dell'Università di Milano.
Suddiviso in quattro aree tematiche - topologia, massimi e minimi, visualizzazione, simmetria - il libro utilizza illustrazioni ed esempi semplici e coinvolgenti.
La sezione sulla topologia esplora il concetto di nodi, mostrando come le modifiche alle curve chiuse non ne alterano la categoria topologica.
La matematica dei massimi e minimi è esemplificata dalla forma circolare delle mura di Milano, che ottimizzano il rapporto tra superficie racchiusa e lunghezza del perimetro.
Il libro dimostra come la matematica sia presente in aspetti inaspettati della vita quotidiana, come la trama di tessuti, reti di fibre ottiche e la finanza.

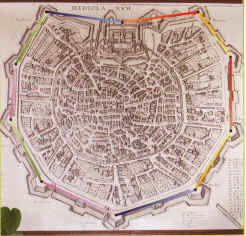Matemilano, percorsi matematici in città
a cura di M. Bertolini, M. ****la, M. Dedò, S. Di Sieno, E. Frigerio, D. Luminati, G. Poldi, M. Rampichini, I. Tamanini, G. M. Todesco, C. Turrini, Springer-Verlag, Milano, 2004

Il libro è in parte il catalogo della mostra Matemilano , ideata e realizzata dal Dipartimento di Matematica dell'Università degli Studi di Milano con la collaborazione del Dipartimento di Matematica dell'Università di Trento, allestita per la prima volta nell'autunno 2003 presso il Museo Nazionale della Scienza e della Tecnologia "Leonardo da Vinci" di Milano.
Il libro, tuttavia, non è un semplice catalogo illustrativo degli 'oggetti' presentati alla mostra ma una raccolta di brevi saggi, semplici da leggere, ricchi di illustrazioni ed esempi, su alcune applicazioni della matematica al mondo dell'esperienza quotidiana, dove per esperienza quotidiana si deve intendere anche una passeggiata in città per osservare, da un punto di vista matematico, palazzi, quadri, mosaici, fregi, tessuti, fibre ottiche, nodi, bolle di sapone, ....
I saggi si sviluppano intorno a quattro aree tematiche: topologia, massimi e minimi, visualizzazione, simmetria.
Uno dei temi più curiosi della topologia riguarda i nodi.

Si prende una corda e si fa un nodo, qualunque esso sia, se i due estremi della corda rimangono liberi, si può sempre riuscire a sciogliere il nodo. Se invece dopo aver fatto il nodo si incollano in qualche modo gli estremi della corda in modo da non poterli più staccare ecco che i nodi cominciano ad assumere una certa personalità topologica.

In altri termini, ogni nodo, anche se lo si modifica quanto si vuole, apparterrà a una categoria ben precisa. Se il nodo può essere sciolto si avrà un semplice cerchio, altrimenti si avrà un nodo "trifoglio" (in alto a destra nella prima immagine), un nodo Savoia (in alto a sinistra), ecc. Ma non si potrà mai trasformare un nodo trifoglio in un nodo Savoia. Un nodo scorsoio, invece, è un finto nodo perché può essere sciolto e trasformato in un cerchio. La topologia è quindi quella branca della matematica che ci permette di catalogare le figure geometriche, nel caso dei nodi le curve chiuse, in modo che modificandole quanto si vuole, senza tagliarle, rimangono sempre nella categoria alla quale appartengono.
Detta così, la questione dei nodi, sembrerebbe una banalità sulla quale non c'è molto altro da dire, eppure la questione è piuttosto complicata ed è ancora un problema matematico non risolto completamente.
La pianta della città di Milano introduce uno dei grandi temi della matematica, quello dei massimi e minimi . La cinta muraria delle antiche città di pianura ha una forma che richiama quella del cerchio. A un osservatore distratto potrebbe sembrare che si tratti di questioni puramente estetiche, invece la circonferenza è la figura geometrica che racchiude la massima superficie con un perimetro minimo. Una protezione circolare è quindi quella che permette di racchiudere la massima superficie minimizzando le mura da difendere.
Il problema, semplice nel caso di un terreno piano, è piuttosto complesso per una città delimitata da un fiume o a ridosso di una montagna.
Nel primo libro dell'Eneide, Virgilio riporta la leggenda della regina Didone. La regina, in fuga con il suo popolo, si rifugiò sulle coste settentrionali dell'Africa e chiese della terra per costruirvi una città. Il re del luogo le concesse tanta terra quanta ne potesse contenere una pelle di toro. Lo scherno si ritorse contro il re, poiché Didone fece tagliare la pelle in strisce sottilissime, con le quali formò una lunga fune che dispose a semicerchio lungo la riva del mare, fondò così la città di Cartagine.
Il libro è ricco di riferimenti ad applicazioni pratiche, anche inaspettate, della matematica: la trama di un tessuto, reti di fibre ottiche, investire con sicurezza i propri risparmi, come misurare la qualità della vita, vedere un nascituro a tutto tondo, ecc.
Il libro, e la mostra, rispondono in modo semplice, chiaro e con tanti esempi a una domanda banale alla quale non sempre si sa rispondere in modo non banale: dov'è la matematica? Leggendo il libro, visitando la mostra, si impara a vederla in casa propria, in città, nella vita di tutti i giorni.

Se non potete andare a Milano potete accontentarvi di una visita virtuale

http://matemilano.mat.unimi.it/presenta.htm

Antonio Bernardo

Domande da interrogazione

Qual è l'obiettivo principale del libro "Matemilano"?

Il libro mira a mostrare come la matematica si applichi al mondo dell'esperienza quotidiana, attraverso saggi semplici e illustrati che esplorano temi come topologia, massimi e minimi, visualizzazione e simmetria.

Quali sono alcune delle applicazioni pratiche della matematica menzionate nel libro?

Il libro menziona applicazioni pratiche come la trama di un tessuto, reti di fibre ottiche, investimenti sicuri, misurazione della qualità della vita e visualizzazione di un nascituro.

Come viene spiegato il concetto di topologia nel contesto dei nodi?

La topologia è descritta come la branca della matematica che classifica le figure geometriche, come i nodi, in categorie specifiche che rimangono inalterate anche se modificate, purché non vengano tagliate.

Qual è l'importanza della forma circolare nelle antiche città di pianura?

La forma circolare è importante perché racchiude la massima superficie con un perimetro minimo, ottimizzando così la protezione con il minor numero di mura da difendere.

Qual è la leggenda di Didone e come si collega al tema dei massimi e minimi?

La leggenda narra che Didone usò una pelle di toro tagliata in strisce per delimitare la terra su cui fondare Cartagine, illustrando il concetto matematico di massimizzare l'area con un perimetro limitato.

Matemilano, percorsi matematici in città