Concetti Chiave
- Bruno D'Amore esplora l'interazione tra matematica e cultura umana attraverso 14 percorsi illustrati e ricchi di citazioni.
- La superformula di Lamé-Gielis permette di modellare numerose forme naturali, dai cristalli alle conchiglie, attraverso specifici parametri.
- Il libro confronta l'ignoranza matematica di alcuni scienziati con la comprensione intuitiva di scrittori come Jonathan Swift.
- Gilbert White osserva erroneamente la natura non seguire proporzioni matematiche, mentre Swift dimostra il contrario nel suo romanzo.
- La proporzione corretta nel rapporto peso/lunghezza conferma che la natura segue armonie matematiche anche negli uccelli.
Bruno D'Amore, Matematica dappertutto. Percorsi matematici inusuali e curiosi, Pitagora Editrice, Bologna, 2007, pp.88 
Bruno D'Amore ci mostra una matematica che ha invaso tutte le altre forme della cultura umana in 14 brevi ma intensi percorsi, ben illustrati e ricchi di citazioni. Per citarne qualcuno: la superformula di Lamé-Gielis
ho =
oot{n_1} {|frac{1}{a}\\cos(frac m 4 \phi)|^{n_2}+|frac 1 b \\sin (frac m 4 \phi)|^{n_3}}[/math]
che con opportuni valori dei parametri a, b, m, n1, n2, n3, permette di ottenere una grande quantità di forme geometriche che effettivamente si incontrano in natura, dai cristalli alle conchiglie, dalle alghe alle foglie.
D'amore ci mostra il confronto tra le forme geometriche disegnate per mezzo della formula e le foto degli oggetti reali.
Divertente anche il capitolo in cui confronta l'ignoranza matematica di alcuni scienziati con le competenze raffinate di alcuni scrittori. Gilbert White (1720-1793) studioso di uccelli, dallo studio di un esemplare di cavaliere, un uccello di palude, dal peso di 120 g e lunghezza delle zampe 20,4 cm, trovò che il rapporto peso/lunghezza delle zampe doveva essere 120:20,4 = 5,8. Quando lo stesso White catturò un fenicottero, simile al cavaliere ma molto più pesante, 1,82 kg su zampe lunghe 50 cm, osservò che la proporzione non era la stessa di quella del cavaliere, il fenicottero avrebbe dovuto infatti avere le zampe di 3m. Da qui White dedusse che la natura non lavora con 'armonia matematica'. Jonathan Swift (1667-1745) nel suo famoso romanzo I Viaggi di Gulliver scrive che quando Gulliver raggiunge il paese di Lilliput, i matematici di questo paese avendo scoperto che la statura di Gulliver eccedeva la loro nella proporzione di dodici a uno, e considerando che i loro corpi erano simili al suo, dedussero che doveva contenere 1728 corpi loro e che quindi Gullier aveva bisogno di tanto cibo quanto ne occorreva per altrettanti lillipuziani. Come mai un naturalista come White non se è reso conto che il peso degli uccelli, va pensato come un volume e quindi va rapportato con il cubo delle lunghezze (quella delle gambe) mentre Swift lo aveva capito? Scrivendo infatti correttamente la proporzione si osserva che la natura lavora armonicamente anche negli uccelli:
.
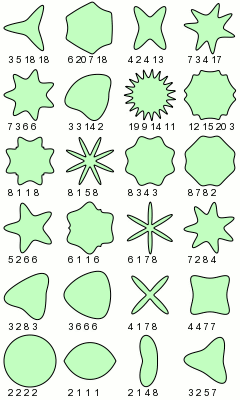
Alcune immagini della superformula per i valori dei parametri indicati. Immagine da http://it.wikipedia.org/wiki/Superformula
Domande da interrogazione
- Qual è l'obiettivo principale del libro di Bruno D'Amore "Matematica dappertutto"?
- Cosa dimostra la superformula di Lamé-Gielis secondo Bruno D'Amore?
- Qual è il confronto tra Gilbert White e Jonathan Swift riguardo alla comprensione matematica?
Il libro di Bruno D'Amore mira a mostrare come la matematica abbia invaso tutte le forme della cultura umana attraverso 14 percorsi brevi ma intensi, illustrati e ricchi di citazioni.
La superformula di Lamé-Gielis, con opportuni valori dei parametri, permette di ottenere una grande quantità di forme geometriche che si incontrano in natura, come cristalli, conchiglie, alghe e foglie, mostrando il confronto tra forme geometriche e oggetti reali.
Gilbert White, un naturalista, non si rese conto che il peso degli uccelli va rapportato con il cubo delle lunghezze, mentre Jonathan Swift, uno scrittore, lo comprese correttamente nel suo romanzo, dimostrando che la natura lavora armonicamente anche negli uccelli.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
