Concetti Chiave
- La decomposizione classica additiva del modello si basa su tre componenti: trend, stagionalità e casualità, verificando gli errori tramite test di specificazione.
- R offre tre funzioni per la decomposizione di serie temporali: decompose() e stl() nel package stats, e tsr() nel package ast.
- La funzione decompose() può essere usata per modelli additivi e moltiplicativi, restituendo componenti come stagionalità, trend ed errori in vettori distinti.
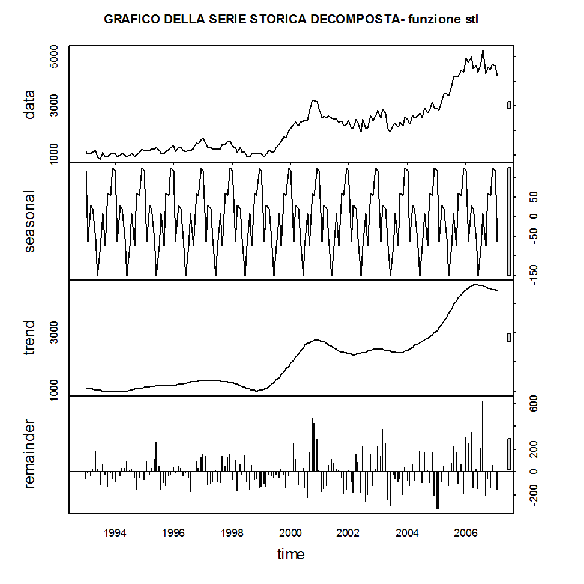
- La funzione stl() utilizza il metodo loess per fornire stime più accurate, memorizzando le componenti in vettori separati per analisi e visualizzazione.
- La funzione tsr() permette di utilizzare diversi smoothers, come loess e spline, per migliorare l'adattamento del trend, con risultati migliori aumentando i parametri equivalenti.
L'approccio più semplice della decomposizione classica è basata sul modello di tipo additivo:
Yt= Tt + St + εt
con εt ~ NID (0,σ2) ovvero supponendo che gli errori siano distribuiti normalmente con media zero e varianza costante e siano tra loro indipendenti. Tali ipotesi saranno verificate tramite appositi tests di specificazione del modello. R consente di determinare e stimare tali componenti con tre diverse funzioni: decompose() e stl() nel package stats, tsr() nel package ast.
Funzione decompose
La funzione decompose() può essere applicata sia al modello additivo che al modello moltiplicativo, per questo occorre specificarlo nel parametro type=c(“additive”, “multiplicative”).
> dec.fit
La funzione restituisce un oggetto con le seguenti componenti:
• seasonal, vettore con la stagionalità
• figure, stima della componente stagionale per i dodici mesi dell'anno
• trend, vettore con il trend della serie
• random, vettore con gli errori.
Si memorizzino in alcuni vettori le tre componenti ottenute:
> stag.dec[math]seasonal>br>> trend.dec>-dec.fit[/math]trend
> res.dec[math]random
Per otte
ere il grafico della decomposizio
e della serie:
> plot(dec.fit)

Funzio
e stl()
La funzio
e stl() fornisce delle stime migliori in quan o per la decomposizio
e usa il me odo loess:
> stl.fit> attributes(stl.fit)
[/math]names
[1] "time.series" "weights" "call" "win" "deg" "jump" "inner" "outer"
[1] \text{stl}
La funzio
e restituisce un ogget o le cui compo
enti possono essere memorizzate in vet ori
> stag.stltime.series[,1]
> trend.stl[math]time.series[,2]>br>> res.stl>-stl.fit[/math]
Il grafico della serie storica decomposta è il seguente
> plot(stl.fit,main="GRAFICO DELLA SERIE STORICA DECOMPOSTA- funzione stl")
Funzione tsr()
Si tratta di un'ulteriore funzione per la decomposizione di una serie temporale. Gli stimatori, detti smoothers, riconosciuti sono:
• constant: la serie assume valore uguale alla media;
• poly(r): la serie viene interpolata con un polinomio di grado r;
• loess(r, g): la serie viene stimata utilizzando una regressione locale di tipo loess;
• gauss(r, g): la serie viene stimata utilizzando una regressione locale con pesi gaussiani;
• spline(g): la serie osservata è stimata utilizzando una spline con g parametri equivalenti.
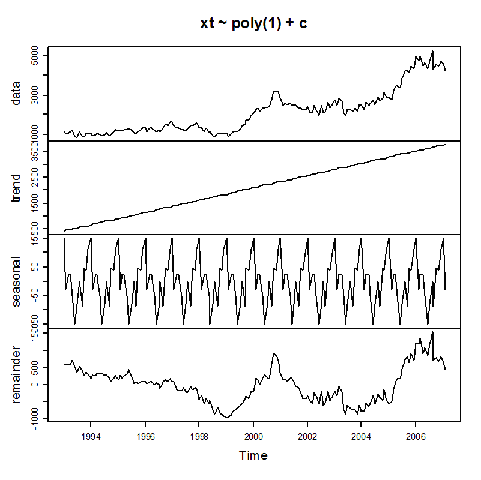
> tsr.fit
Per avere una visualizzazione grafica del modello stimato:
> plot(tsr.fit)
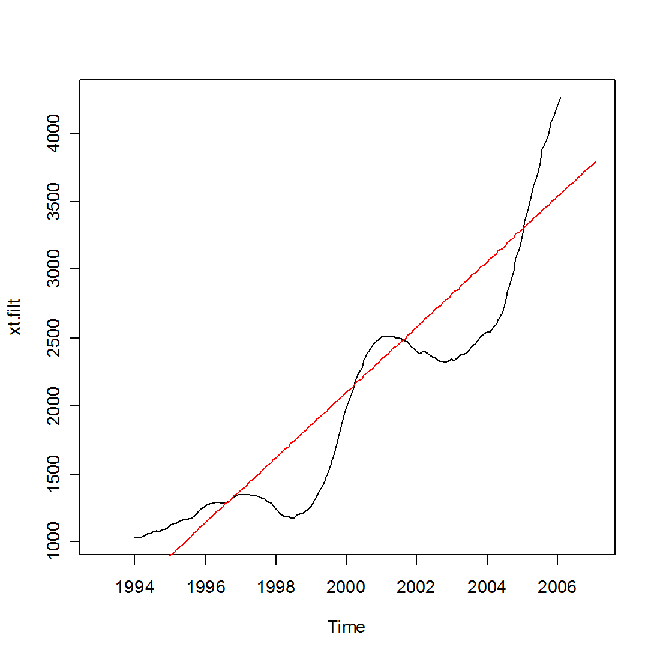
Si valuti il grado di adattamento di questo tipo di trend tracciando il grafico della serie filtrata sovrapposto al trend stimato con tsr():
> plot(xt.filt)
> lines(trend(tsr.fit),col="red")
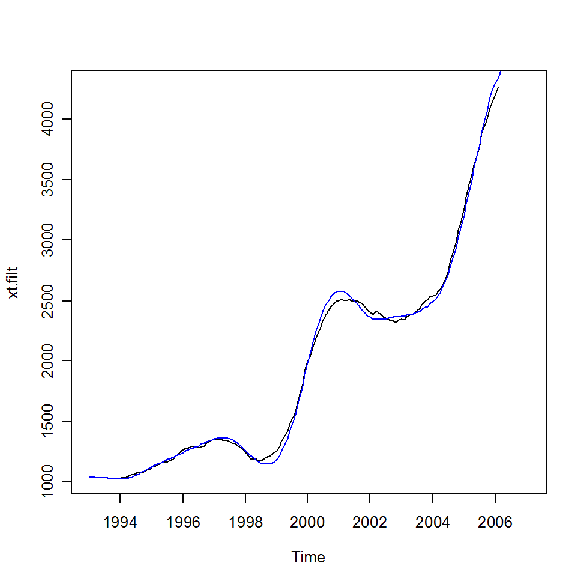
Come si può facilmente vedere l'adattamento non è particolarmente buono e ciò induce all'utilizzo di un altro tipo di stimatore, ad esempio di tipo loess:
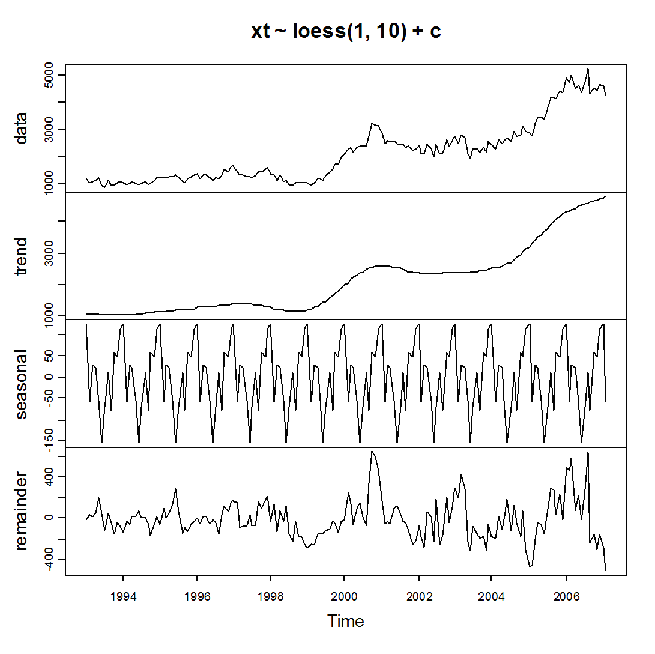
> tsr2.fit> plot(tsr2.fit)
Si valuti il grado di adattamento:
> plot(xt.filt)
> lines(trend(tsr2.fit),col="blue")
Il risultato è decisamente migliore. Per determinare il numero dei parametri spesso si deve procedere per tentativi, ma in generale aumentando il numero dei parametri equivalenti il grado di adattamento migliora.
Si confrontino i trend stimati con i tre metodi:
> plot(trend(tsr2.fit),main="COMPARAZIONE DEL TREND STIMATO")
> lines(xt.filt,col="red")
> lines(trend.stl,col="green")
Si proceda alla memorizzazione delle componenti risultanti dalla funzione tsr() in tre vettori distinti
> trend.tsr> stag.tsr> res.tsr
Domande da interrogazione
- Qual è il modello di decomposizione classica descritto nel testo?
- Quali funzioni di R sono menzionate per la decomposizione delle serie temporali?
- Come si differenzia la funzione stl() rispetto a decompose()?
- Quali sono gli stimatori riconosciuti dalla funzione tsr()?
Il modello di decomposizione classica descritto è di tipo additivo: Yt = Tt + St + εt, dove gli errori εt sono distribuiti normalmente con media zero e varianza costante e sono indipendenti tra loro.
Le funzioni menzionate sono decompose() e stl() nel package stats, e tsr() nel package ast.
La funzione stl() fornisce stime migliori utilizzando il metodo loess per la decomposizione, mentre decompose() può essere applicata sia al modello additivo che al modello moltiplicativo.
Gli stimatori riconosciuti dalla funzione tsr() sono constant, poly(r), loess(r, g), gauss(r, g), e spline(g).






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo