Concetti Chiave
- Il Folium di Cartesio è un esempio di funzione implicita, rappresentata dall'equazione x^3 + y^3 - 3*x*y = 0.
- Per graficare il Folium di Cartesio con Mathcad, si consiglia di utilizzare il comando "Contour Plot".
- Il "Contour Plot" permette di visualizzare la funzione implicita come curva di livello di una superficie tridimensionale.
- È necessario impostare gli estremi dell'intervallo e il numero di divisioni per le variabili x e y.
- La funzione può essere rappresentata anche in forma parametrica razionale, offrendo un'alternativa alla rappresentazione implicita.
Grafico del Folium di Cartesio con Mathcad ( Carlo Elce )
Le funzioni implicite in x e y sono quelle funzioni in cui non è facile isolare una variabile in funzione dell'altra. Per esempio, consideriamo il Folium di Cartesio la cui equazione è x^3 + y^3 -3*x*y = 0.
Per graficare questa funzione con Mathcad è consigliabile usare il comando "Contour Plot". In questo modo si riuscirà ad ottenere il grafico della funzione implicita come curva di livello di una superficie dello spazio a tre dimensioni.
parametro variabile
Estremi dell'intervallo in cui deve variare x :
Immettiamo il numero di divisioni dell'intervallo in cui deve variare x :
Estremi dell'intervallo in cui deve variare y :
Immettiamo il numero di divisioni dell'intervallo in cui deve variare y :
:
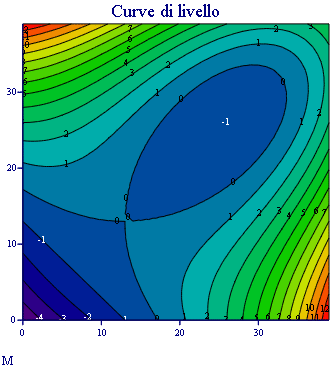
Grafico del Folium di Cartesio con Mathcad ( Carlo Elce )
Le funzioni implicite in x e y sono quelle funzioni in cui non è facile isolare una variabile in funzione dell'altra. Per esempio, consideriamo il Folium di Cartesio la cui equazione è x^3 + y^3 -3*x*y = 0.
Per graficare questa funzione con Mathcad è consigliabile usare il comando "Contour Plot". In questo modo si riuscirà ad ottenere il grafico della funzione implicita come curva di livello di una superficie dello spazio a tre dimensioni.
parametro variabile
Estremi dell'intervallo in cui deve variare x :
Immettiamo il numero di divisioni dell'intervallo in cui deve variare x :
Estremi dell'intervallo in cui deve variare y :
Immettiamo il numero di divisioni dell'intervallo in cui deve variare y :
:
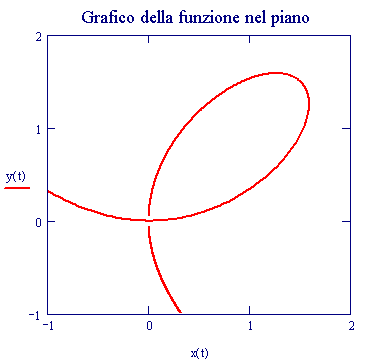
La funzione di cui sopra ammette una rappresentazione parametrica razionale:
E pertanto:
La funzione di cui sopra ammette una rappresentazione parametrica razionale:
E pertanto:
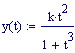
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
