Ominide

1 min. di lettura

Vota 3,3 / 5

set terminal png medium size 480,480
set output "cissoide.png"
set polar
set size ratio 1
set zeroaxis ls 1
set xrange [-2:2]
set yrange [-2:2]
a = 1.2
plot a*(sin(t-a/2)**2/cos(t)) notitle with line lc "black" lw 2
set output

Recensioni

3,3/5

3 recensioni

5 stelle

4 stelle

3 stelle

2 stelle

1 stella

Ti è piaciuto questo appunto?

Lovecchio Ing. Filomeno

BARICENTRO della superficie della CISSOIDE per a=2,
= 2.integrale da 0 a xG della
radice(x^3:sad:2-x)).dx=
=(9,42477796/2)=4,71238898.
La primitiva della funzione integranda è impossibile determinarla.
Con un calcolatore portatile,
non di facile uso,
xG=1.8080948366 ; yG=0.
Delle parti positiva e negativa della CISSOIDE,le
ordinate dei baricentri sono
+,-radice((1,808948366)^3/(2-1,808948366))=+,-5,56626499.

8 Marzo 2012

Lovecchio Ing. Filomeno

Premesso che la "podaria" di una funzione è il luogo geometrico dei piedi delle perpendicolari condotte da un punto qualunque alle tangenti della funzione,mi preme precisare che,nel caso in esame, la "podaria cissoide" della parabola è il relativo "luogo geometrico" dei piedi delle perpendicolari condotte dal vertice della parabola alle relative tangenti.

21 Novembre 2011

Lovecchio Ing. Filomeno

La "cissoide" è formata di due curve uguali,simmetriche rispetto agli assi cartesiani,il cui campo di
esistenza è (0 ; +,-a(.
L'equazione cartesiana di una cissoide è a.y^2-x.y^2=x^3,
da cui
y=+,-radice(x^3:sad:a-x)).
L'equazione polare di una "cissoide= è
rho=a(sen.tetha)^2:cos.theta,
che si dimostra ,sostituendo alla x e alla y dell'equazione cartesiana
x=rho(cos.theta),
y=rho(sen.tetha).
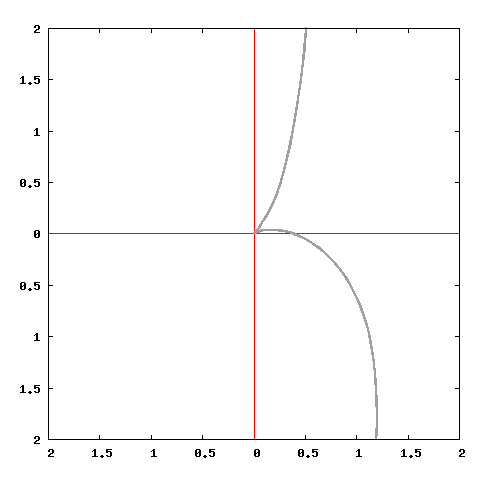
In figura non è riportata una cissoide , ma due curve , le cui equazioni sono
y=+radice(x^3:sad:0,53125-x);
y=-radice(x^3:sad:2-x)).
Inoltre una "cissoide" non interseca l'asse x o l'asse y,
come in figura.
La "cissoide" è la "podaria" di una parabola ; dell'equazione della parabola
y=(1/4)x^2 ,
l'equazione della relativa podaria è
x=-radice(y^3:sad:2-y));
a=2,ordinata del fuoco della parabola.

17 Novembre 2011

Domande e risposte

Hai bisogno di aiuto?

Chiedi alla community

Fai una domanda

Cissoide

set terminal png medium size 480,480 set output "cissoide.png" set polar set size ratio 1 set zeroaxis ls 1 set xrange [-2:2] set yrange [-2:2] a = 1.2 plot a*(sin(t-a/2)**2/cos(t)) notitle with line lc "black" lw 2 set output

Recensioni

Domande e risposte

Quali linguaggi di programmazione consigli per iniziare nel 2024?

help c+++

Programma in C (310905)

I migliori insegnanti di Informatica

Salvatore F.

Andrea D.

Appunti correlati

Software assembly

Verifica se una parola è palindroma in C++ - Codice e funzionamento

Vantaggi e caratteristiche delle reti informatiche: efficienza, sicurezza e risparmio

Sicurezza informatica - Principali tipologie di malware

Recensioni

Domande e risposte

Quali linguaggi di programmazione consigli per iniziare nel 2024?

help c+++

Programma in C (310905)

I migliori insegnanti di Informatica

Salvatore F.

Andrea D.