In prossimità di una distribuzione piana infinita di carica, una carica q = 2,6 * 10^(-6) C risente di una forza F_1 = 40 N . La densità di carica superficiale varia da un valore iniziale σ_1 fino a un valore finale σ_2

_francesca.ricci
di _francesca.ricci
2 min
Erectus
Vota
Appunto verificato
Contenuto verificato e approvato dal  Team di Esperti di Skuola.net Informazioni appunto verificato Informazioni appunto verificato hover

Calcolare la variazione di densità superficiale di una distribuzione piana infinita di carica con densità di carica variabile.

Concetti Chiave

  • Una carica q di 2,6 x 10-6 C è influenzata da due forze, F1 di 40 N e F2 di 70 N, entrambe nella stessa direzione.
  • La densità di carica superficiale varia da un valore iniziale σ1 a un valore finale σ2, modificando la forza sulla carica.
  • Utilizzando la formula del campo elettrico E = σ / (2ε), si calcola σ come E · 2ε, dove E = F / q.
  • Calcolata la densità di carica iniziale σ1 come 272,4 x 10-6 C/m2 e la densità finale σ2 come 476,75 x 10-6 C/m2.
  • La differenza tra le due densità di carica, Δσ, risulta essere 2,0 x 10-4 C/m2.
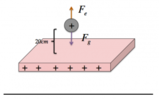
In prossimità di una distribuzione piana infinita di carica, una carica
[math]q = 2,6 \cdot 10^{-6} C [/math]
risente di una forza
[math]F_1 = 40 N [/math]
.

La densità di carica superficiale varia da un valore iniziale

[math] \sigma_1 [/math]
fino a un valore finale
[math] \sigma_2 [/math]
e, alla fine, la stessa carica subisce una forza
[math]F_2 = 70 N [/math]
che ha lo stesso verso della forza
[math]F_1[/math]
.

Determina la differenza fra le due densità di carica

[math]∆ \sigma = \sigma_2 - \sigma_1 [/math]
.

Svolgimento

Per determinare la densità di carica, consideriamo la formula
[math]E = \frac{\sigma}{2 \epsilon} [/math]
che descrive l’intensità del campo elettrico nel caso di una superficie piana infinita di carica.

Ricaviamo la densità:

[math] E = \frac{\sigma}{2 \epsilon} \to \sigma = E \cdot 2\epsilon [/math]

Possiamo esprimere il campo elettrico come

[math] E = \frac{F}{q}[/math]
:

[math] \sigma = E \cdot 2 \epsilon = \frac{F}{q} \cdot 2 \epsilon [/math]

Applichiamo questa formula nel primo e nel secondo caso, cioè nei casi delle due diverse forze:

[math] \sigma_1 = \frac{F_1}{q} \cdot 2 \epsilon = \frac{40 N}{2,6 \cdot 10^{-6} C} \cdot 2 \cdot 8,854 \cdot 10^{-12} \frac{C^2}{N \cdot m^2} = [/math]

[math] 272,4 \cdot 10^{-6} \frac{C}{m^2} [/math]

[math] \sigma_2 = \frac{F_2}{q} \cdot 2 \epsilon = \frac{70 N}{2,6 \cdot 10^{-6} C} \cdot 2 \cdot 8,854 \cdot 10^{-12} \frac{C^2}{N \cdot m^2} = [/math]

[math] 476,75 \cdot 10^{-6} \frac{C}{m^2} [/math]

Determiniamo quindi la differenza fra le due densità:

[math] ∆ \sigma = \sigma_2 - \sigma_1 = 476,75 \cdot 10^{-6} \frac{C}{m^2} - 272,4 \cdot 10^{-6} \frac{C}{m^2} = [/math]

[math] 2,0 \cdot 10^{-4} \frac{C}{m^2} [/math]

Domande da interrogazione

  1. Come si calcola la densità di carica superficiale in una distribuzione piana infinita di carica?

    2. La densità di carica superficiale si calcola utilizzando la formula \( \sigma = \frac{F}{q} \cdot 2 \epsilon \), dove \( F \) è la forza, \( q \) è la carica e \( \epsilon \) è la costante dielettrica del vuoto.

  2. Quali sono i valori delle densità di carica superficiale iniziale e finale?

    3. La densità di carica superficiale iniziale è \( \sigma_1 = 272,4 \cdot 10^{-6} \frac{C}{m^2} \) e quella finale è \( \sigma_2 = 476,75 \cdot 10^{-6} \frac{C}{m^2} \).

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Vai al forum