La disequazione è equivalente alle due disequazioni:
Studiamo singolarmente le due disequazioni
1)
2)
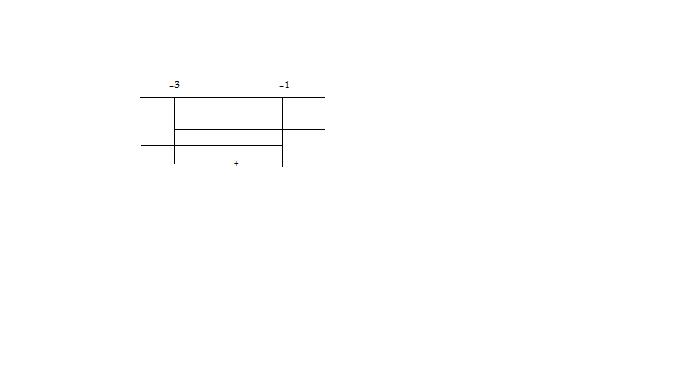
Poiché dobbiamo considerare l'unione degli insiemi ottenuti, la disequazione é verificata per
Processo di Validazione
Ogni contenuto pubblicato su Skuola.net è sottoposto a un processo di validazione in tre fasi, per garantirne originalità, accuratezza e qualità:
Studiamo singolarmente le due disequazioni
1)
2)
Poiché dobbiamo considerare l'unione degli insiemi ottenuti, la disequazione é verificata per

5 stelle
4 stelle
3 stelle
2 stelle
1 stella
0
1
0
0
0
x inferiore a -1.x superiore a -3.bisogna fare l intersezione per -3
Sei già abbonato? Accedi

3,99€
 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo
 Nessuna pubblicità sul sito
Nessuna pubblicità sul sito
 100€ di bonus su Ripetizioni.it
100€ di bonus su Ripetizioni.it
Disdici quando vuoi
7,99€
 5 appunti ogni mese
5 appunti ogni mese
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo
 Nessuna pubblicità sul sito
Nessuna pubblicità sul sito
 100€ di bonus su Ripetizioni.it
100€ di bonus su Ripetizioni.it
Disdici quando vuoi
12,79€
 3 appunti ogni mese
3 appunti ogni mese
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo
 Nessuna pubblicità sul sito
Nessuna pubblicità sul sito
 100€ di bonus su Ripetizioni.it
100€ di bonus su Ripetizioni.it
Disdici quando vuoi
Hai cambiato idea e vuoi dare il consenso?
Vuoi copiare questo testo?