Circuiti Integratori

di kykko_90

Ominide

4 min. di lettura

Vota 3 / 5

Concetti Chiave

Il circuito integratore invertente utilizza il principio della massa virtuale per calcolare la tensione di uscita in base alla tensione di ingresso.
La tensione di uscita del circuito integratore invertente è in anticipo di 90 gradi rispetto alla tensione di ingresso, con l'ampiezza che aumenta al diminuire della frequenza.
Il circuito integratore non invertente utilizza quattro resistenze uguali e un condensatore, con reazioni sia negative che positive.
Nel circuito integratore non invertente, la tensione di uscita è in ritardo di 90 gradi rispetto alla tensione di ingresso, con il modulo che aumenta al diminuire della frequenza.
Sia per la configurazione invertente che per quella non invertente, la trasformata di Laplace è utilizzata per derivare le formule della tensione di uscita.

Circuiti Integratori

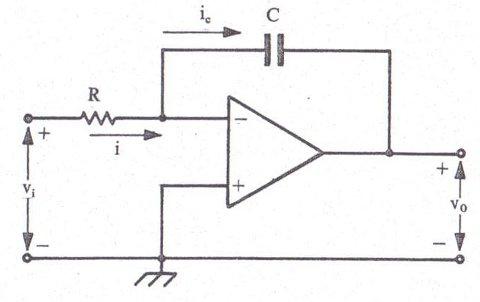
Lo schema sovrastante mostra un circuito integratore nella configurazione invertente. Si utilizza per le operazioni di integrazione.
Qui sotto è riportato l'andamento delle forme d'onda che escono dall'integratore.

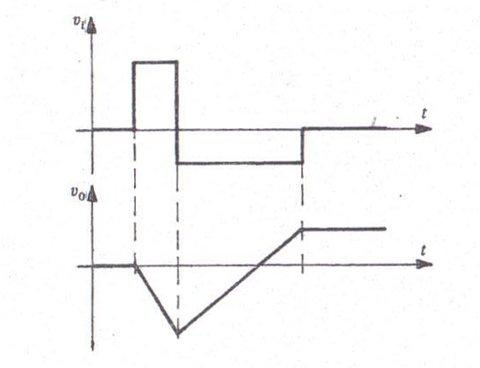
Se dobbiamo ricavare

[math]v_o\left(t\right)[/math]

in funzione di

[math]v_i\left(t\right)[/math]

si applica il principio della massa virtuale, quindi la corrente erogata dal generatore

[math]v_i\left(t\right)[/math]

vale:

[math]i=\frac{v_i\left(t\right)}{R}[/math]

e coincide con la corrente che attraversa il condensatore.
La tensione ai capi del condensatore invece vale:

[math]v_c\left(t\right)=\frac{q\left(t\right)}{C}=\frac{1}{c}\int_{0}^{t}i_c\left(t\right) dt=\frac{1}{C}\int_{0}^{t}\frac{v_i\left(t\right)}{R} dt=\frac{1}{R \cdot C}\int_{0}^{t}v_i\left(t\right)dt[/math]

[math]v_c\left(t\right)=v_n-v_0\left(t\right)=-v_0\left(t\right)[/math]

per cui otteniamo che:

[math]v_0\left(t\right)=-\frac{1}{R\cdot C} \int_{0}^{t}v_i\left(t\right)dt[/math]

adoperando la trasformata di Laplace e subito dopo l'anti-trasformata otteniamo:

[math]V_0\left(j\omega \right)=-\frac{1}{j \omega RC}\cdot V_i=j\cdot \frac{V_i}{\omega RC}[/math]

Da quest'ultima formula possiamo notare che

[math]V_0[/math]

è in anticipo di

[math]90^\circ[/math]

rispetto a

[math]V_i[/math]

e che a parità di

[math]R[/math]

e di

[math]C[/math]

, l'ampiezza della tensione di uscita aumenta al diminuire della frequenza di ingresso

[math]\omega[/math]

Andiamo adesso ad analizzare il circuito di un integratore nella configurazione non invertente riportato qui sotto.

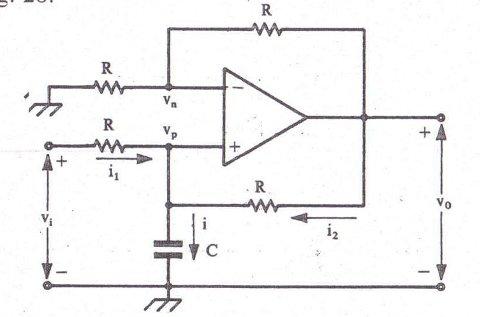
Il circuito è composto da quattro resistenze

[math]R[/math]

uguali ed un condensatore e presenta una reazione sia negativa che positiva.
L'espressione di

[math]v_0[/math]

in funzione di

[math]v_i[/math]

si ricava con il metodo dell'equipotenzialità degli amplificatori operazionali, poi applichiamo il I° principio di Kirchhoff al morsetto non invertente e otteniamo:

[math]i=i_1+i_2=\frac{v_i-v_p}{R}+\frac{v_0-v_p}{R}=\frac{v_i+v_0-2v_p}{R}[/math]

però siccome:

[math]v_p=v_n=v_0\cdot \frac{R}{2R}=\frac{v_0}{2}[/math]

e quindi

[math]i=\frac{v_i}{R}[/math]

La tensione ai capi del condensatore

[math]v_p[/math]

ci da che:

[math]v_0=2\cdot v_p=\frac{2q}{C}=\frac{2}{C}\int_{0}^{t} i\left(t\right) dt=\frac{2}{RC}\int_{0}^{t} v_i\left(t\right) dt[/math]

Dopo aver applicato Laplace arriviamo allo stesso risultato e per ricavare il potenziale applichiamo Millmann al morsetto non invertente ed otteniamo:

[math]V_p=\frac{\frac{V_i}{R}+\frac{V_0}{R}}{\frac{1}{R}+s\cdot C+\frac{1}{R}}=\frac{V_i+V_0}{2+sRC}[/math]

Siccome

[math]V_p=V_n=\frac{V_0}{2}[/math]

abbiamo:

[math]V_0\cdot\left(2+sRC\right)=2\cdot\left(V_i+V_0\right)[/math]

da cui ricaviamo:

[math]V_0=\frac{2}{CR}\cdot\frac{V_i}{s}[/math]

se anti-trasformiamo ritroviamo la seguente formula:

[math]v_0=2\cdot v_p=\frac{2q}{C}=\frac{2}{C}\int_{0}^{t} i\left(t\right) dt=\frac{2}{RC}\int_{0}^{t} v_i\left(t\right) dt[/math]

Se si porta la seguente formula

[math]\left(V_0=\frac{2}{CR}\cdot\frac{V_i}{s}\right)[/math]

in regime sinusoidale e, si pone

[math]s=j\omega[/math]

troviamo:

[math]V_0=\frac{2\cdot V_i}{j\omega RC}[/math]

Notiamo che

[math]V_0[/math]

è in ritardo di

[math]90^\circ[/math]

rispetto a

[math]V_i[/math]

e come per la configurazione invertente il modulo aumenta al diminuire della sua frequenza. integratore-invertente

Domande da interrogazione

Qual è la funzione principale di un circuito integratore nella configurazione invertente?

Un circuito integratore nella configurazione invertente viene utilizzato per eseguire operazioni di integrazione, trasformando un segnale di ingresso in un segnale di uscita che rappresenta l'integrale del segnale di ingresso nel tempo.

Come si comporta la tensione di uscita [math]V_0[/math] rispetto alla frequenza di ingresso [math]\omega[/math] nel circuito integratore invertente?

Nel circuito integratore invertente, l'ampiezza della tensione di uscita [math]V_0[/math] aumenta al diminuire della frequenza di ingresso [math]\omega[/math], e [math]V_0[/math] è in anticipo di [math]90^\circ[/math] rispetto a [math]V_i[/math].

Qual è la differenza principale tra le configurazioni invertente e non invertente di un circuito integratore?

La configurazione invertente presenta un'uscita [math]V_0[/math] in anticipo di [math]90^\circ[/math] rispetto a [math]V_i[/math], mentre nella configurazione non invertente [math]V_0[/math] è in ritardo di [math]90^\circ[/math] rispetto a [math]V_i[/math]. Entrambe le configurazioni mostrano un aumento del modulo al diminuire della frequenza.

Circuiti Integratori