2016 Tema di matematica Scientifico opzione Scienze Applicate [M557]

PROBLEMA 1

1. Discuti campo di esistenza, continuità e derivabilità della funzione
   [math]G(x)[/math]
   . Individua gli intervalli di positività/negatività e le eventuali intersezioni con gli assi cartesiani.
2. Determina l’esistenza degli asintoti della funzione
   [math]G(x)[/math]
   , motivando opportunamente la risposta.
3. Individua i punti stazionari della funzione
   [math]G(x)[/math]
   , riconoscendone la tipologia, e i punti di flesso. Disegna quindi il grafico della funzione, motivando le scelte fatte.
4. Studia l'andamento dei coefficienti angolari delle rette tangenti alla funzione
   [math]G(x)[/math]
   nei suoi punti di flesso a tangente obliqua, determinando in particolare se tali rette formano un fascio di rette parallele.

PROBLEMA 2

1. Relativamente al grafico (Gamma), mostra come variano le coordinate del suo punto di flesso
   [math]P[/math]
   in funzione del parametro
   [math]k[/math]
   e verifica che in tale punto la pendenza del grafico è indipendente da
   [math]k[/math]
   .
2. Dopo aver verificato che la funzione
   [math]p(x) = \log(1+k\cdot e^{-x})+x[/math]
   è una primitiva di
   [math]f[/math]
   , determina l'area della regione piana compresa tra
   [math]\Gamma[/math]
   , l'asse
   [math]y[/math]
   , l’asse
   [math]x[/math]
   e la retta di equazione
   [math]x = \log(\alpha)[/math]
   . Che valore deve assumere
   [math]alpha[/math]
   perché tale area sia uguale a 1?
3. Dimostra che
   [math] g(x) = \log\Big(\frac{kx}{1-x}\Big) [/math]
   è la funzione inversa di
   [math]f[/math]
   e tracciane il grafico. Prova inoltre che la suddetta funzione
   [math]g[/math]
   è crescente in tutto il suo dominio e che il grafico della funzione
   [math]h[/math]
   , definita come
   [math] h(x) = f(x)+g(x) [/math]
   interseca l’asse
   [math]x[/math]
   in un unico punto.
4. Considerata, per
   [math]x \in \mathbb{R} [/math]
   , la funzione
   [math] F(x) = \int_0^x f(t), dt [/math]
   determina le equazioni dei suoi asintoti e traccia il grafico di
   [math]F(x)[/math]
   .

QUESTIONARIO

1. Tre circonferenze di raggio 1 sono tangenti esternamente una all’altra. Qual è l’area della regione interna che esse delimitano?
2. In un’urna ci sono 20 biglie, ognuna delle quali è rossa o nera. Stabilire quante sono quelle nere, sapendo che estraendo 2 biglie senza riporre la prima estratta, la probabilità di estrarre almeno una biglia nera è 27/38.
3. Dato un cilindro equilatero e la sfera ad esso circoscritta, qual è la probabilità che un punto interno alla sfera cada all'interno del cilindro?
4. Un solido ha per base la regione R del piano cartesiano compresa tra il grafico della funzione:
   [math] f(x) = \frac{1}{x^2+1} [/math]
   e l’asse delle x nell’intervallo [0, 3]; le sue sezioni ottenute su piani perpendicolari all’asse x sono tutti triangoli isosceli di altezza
   [math]kx[/math]
   , con
   [math] k \in \mathbb{R} [/math]
   . Determinare
   [math]k[/math]
   in modo che il volume del solido sia pari a 2.
5. Il grafico di un polinomio di 3° grado è tangente all'asse
   [math]d[/math]
   nell'origine e interseca nuovamente l'asse in un punto di ascissa positiva. L'ascissa e l'ordinata del punto di massimo relativo sono tra loro uguali e diverse da 0. Determinare l'area della regione piana limitata che è compresa tra l'asse
   [math]x[/math]
   e il grafico del polinomio, sapendo che anche tale area coincide numericamente con il valore comune all'ascissa e all'ordinata nel punto di massimo.
6. Il grafico in figura è quello della derivata prima
   [math]f'(x)[/math]
   di una funzione
   [math]f(x)[/math]
   continua in
   [math]\mathbb{R}[/math]
   . Il grafico riportato è simmetrico rispetto all’origine ed ha come asintoti le rette di equazione
   [math]x=0[/math]
   e
   [math]5x+2y=0[/math]
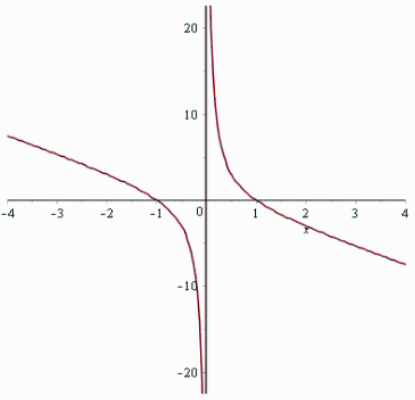   Descrivere le principali caratteristiche relative all’andamento della funzione
   [math]f(x)[/math]
   e tracciarne, indicativamente, un possibile grafico. Tracciare inoltre il grafico della funzione
   [math]f''(x)[/math]
7. Sono date le funzioni
   [math]f(x) = e^{3-x}[/math]
   e
   [math]g(x) = e^{2x}[/math]
   . Determinare l’area della regione limitata racchiusa dall’asse
   [math]x[/math]
   e dai grafici di
   [math]f[/math]
   e di
   [math]g[/math]
   .
8. Un giocatore di basket si esercita ai tiri liberi. Normalmente ha una quota di canestri dell’80%. Con quale probabilità va a canestro esattamente due volte su tre tiri?
   Individua un evento E per il quale valga:
   [math] P(E) = \begin{pmatrix} 50 \ 50 \end{pmatrix} \cdot 0.8^{40} \cdot 0.2^{10} [/math]
9. Dati i punti (4, 14, 17), (16, 11, 14), (16, 2, 23):
   a) si dimostri che il triangolo ABC è isoscele e rettangolo;
   b) quali sono le coordinate del punto D tale che ABCD sia un quadrato?
10. Si considerino nello spazio il punto (1, 2, -1) ed il piano
    [math]\alpha[/math]
    di equazione
    [math] x-2y+z+4=0 [/math]
    .
    a) Verificare che
    [math]P \in \alpha[/math]
    ;
    b) determinare le equazioni delle superfici sferiche di raggio 6 che sono tangenti ad
    [math]\alpha[/math]
    in
    [math]P[/math]
    .