Trigonometria: 1° teorema sui triangoli rettangoli
Con "trigonometria" si intende lo studio dei triangoli rettangoli e delle loro proprietà mediante gli strumenti del calcolo goniometrico.
Triangoli rettangoli: Primo teorema della Trigonometria.
-
"In un triangolo rettangolo, un cateto si ottiene moltiplicando l'ipotenusa per il seno dell'angolo opposto oppure per il coseno dell'angolo adiacente"
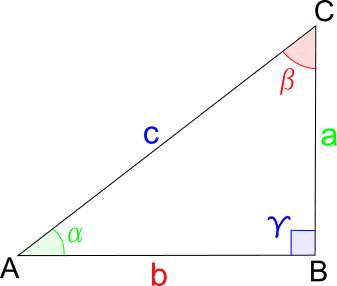
a = c sen α
a = c cos β
b = c sen β
b = c cos α
DIMOSTRAZIONE
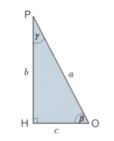
Fissiamo un sistema di riferimento con l'origine fissata nel punto A; l'asse delle ascisse coincide con la retta che passa per A e per B, quindi su cui giace il segmento AB. Disegniamo una circonferenza goniometrica {excursus: una particolare circonferenza che ha il centro C coincidente con l'origine degli assi o(0;0) e raggio r = 1}. La circonferenza goniometrica intersecherà l'ipotenusa nel punto di coordinate P(cosα ; senα). Tracciamo la proiezione del punto P sull'asse delle ascisse, H.
Adesso consideriamo i triangoli che si vengono a formare: APH ed ABC. Essi hanno tutti gli angoli congruenti, quindi avranno i lati in proporzione:BC : PH = AB : AP
a : sen α = c : 1
a = c sen α
- AC : AH = AB : AP
b : cos α = c : 1
a = c cos α
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
