Una ipotesi fittizia può spiegare molti fenomeni [Eulero]

"E poiché la costruzione dell'universo è perfetta ed è opera di un Creatore di immensa saggezza, nulla in esso ha luogo in cui non compaia qualche legge di massimo o minimo". "Anche se non ci è permesso di penetrare negli intimi misteri della natura per apprendere le vere cause dei fenomeni, può nondimeno accadere che una certa ipotesi fittizia sia sufficiente a spiegare molti fenomeni", Leonhard Euler 1707-1783.
"Quando il mio cervello suscita nella mia coscienza la sensazione di un albero o di una casa, io dichiaro, senza esitazione, che un albero o una casa esistono realmente al di fuori di me, e di essi io conosco il luogo, la dimensione e le altre caratteristiche. Pertanto non si trovano né uomini né animali che mettano in dubbio tale verità. Se un contadino potesse concepire di avere tali dubbi e sostenesse, ad esempio, di non credere nell'esistenza del suo controllore e giudice nel momento in cui egli è davanti a lui, sarebbe giustamente preso per pazzo; ma quando un filosofo propone riflessioni di questa natura, egli si aspetta che noi ammiriamo la sua sapienza e la sua sagacia, poiché esse sono infinitamente superiori a quelle della gente comune". (Euler: Lettere a una principessa della Germania: confutazione degli idealisti)
Lo svizzero Leonardo Eulero contende ad Archimede, Newton e Gauss la fama del più grande matematico di tutti i tempi. Certamente i suoi interessi furono vastissimi e spaziano dalla matematica pura a quella applicata, dalla teoria dei numeri, all'analisi infinitesimale al problem solving. Eulero, diversamente da altre persone di genio, fu compreso dai propri contemporanei. Johann Bernoulli in una lettera a lui indirizzata scrisse: "Io presento l'analisi superiore come se essa fosse nella sua fanciullezza, ma voi la state portando alla maturità". Pierre Simon de Laplace ripeteva: "Leggete Euler, leggete Euler, egli è il maestro di noi tutti".
Come matematico si occupo di: serie infinite, geometria differenziale, funzioni complesse, frazioni continue, calcolo delle variazioni, equazioni differenziali, logica degli insiemi, ecc. Come fisico di: propagazione del suono, corde vibranti, natura del calore, canali e opere idrauliche, ingegneria navale, ecc.
Eulero scrisse più di 200 libri e fu certamente il matematico più prolifico in molti rami di questo sapere: ci sono le formule di Euler, i polinomi di Euler, le costanti di Euler, gli integrali euleriani, le rette di Euler, ecc.. Si potrebbe pensare che questo enorme volume di attività escludesse Eulero da qualunque altro interesse nella vita, ma non fu così. Euler si sposò, ebbe tredici figli e fu sempre attento alla sua famiglia e ai suoi bisogni. Educò personalmente figli e nipoti, costruì per loro giochi scientifici e passò molte serate a leggere o riassumere i racconti della Bibbia. Anche se non aveva mai studiato filosofia, e un giorno rimpianse di non averlo fatto, amava esprimere le sue opinioni (vedi ad esempio le Lettere a una principessa della Germania) attirandosi le critiche del terribile Voltaire, che per altro se la prese anche con Leibnitz identificato con il dott. Pangloss afflitto da inguaribile ottimismo.
Un grande contributo di Eulero alla matematica applicata e alla soluzione di problemi fu l'uso di un linguaggio e di una notazione che per molti aspetti corrispondono a quelli usati oggi: nessun matematico, da solo, contribuì in così larga misura come lui, con la felice invenzione di notazioni, a dare alla matematica la forma che essa presenta ancora oggi. Tra i risultati, che hanno anche forte valenza applicativa per le organizzazioni e per l'economia, è da ricordare il concetto e la notazione moderna di funzione [y = f(x1, x2,....)] ed il relativo calcolo dei massimi e minimi impostato in maniera generalizzata e non solo per problemi specifici come avevano fatto Keplero ed altri.
Eulero generalizzò anche il concetto di punti estremi e quello di funzioni estremizzanti dando la prima trattazione sistematica del calcolo delle variazioni. Tra le tecniche di risoluzione dei problemi messe a punto da Euler vi fu lo sviluppo del metodo algoritmico. Esso funzionava in modo tale da ottenere in prima istanza un risultato approssimativo che però poteva essere reinserito nell'algoritmo in modo che risultasse un poco più preciso. Questo secondo risultato poteva essere di nuovo sottoposto all'algoritmo per generare un altro risultato ancora più preciso e così via. Due secoli dopo, con l'avvento dei computer, questo modo di procedere divenne la base per risolvere una vasta classe di problemi di calcolo numerico.

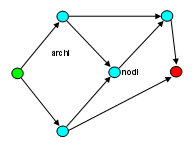
La teoria dei grafi si classifica come capitolo della topologia, in pratica si tratta (vedi figura) di strutture geometriche in cui un insieme di nodi è collegato da un insieme di archi. Il primo scritto su di essi comparve nel 1736 ad opera di Eulero. Oggi I grafi consentono di modellare e studiare una grande quantità di sistemi (trasporto, assegnazione, flusso, progettazione, produzione, ecc.) e di reti (elettriche, stradali, ferroviarie, aeroportuali, sociali, informatiche, ecc.). Essi costituiscono anche la base delle tecniche reticolari di programmazione dei progetti.