L'induzione matematica [Peano]

Giuseppe Peano (1858-1923) partiva dai concetti non definiti di "insieme", "numero naturale", "successore" e "appartiene a". I suoi cinque assiomi per i numeri naturali sono:
1) "Zero è un numero, ma non è successore di alcun numero."
2) "Il successore di ciascun numero è anch'esso un numero."
3) "Ciascun numero ha un solo successore."
4) "Due numeri i cui successivi sono uguali, sono essi stessi uguali."
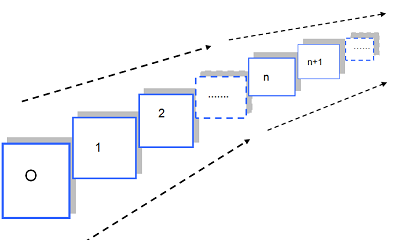
5) "Principio di induzione matematica: se una proprietà P vale per zero e se si può dimostrare che, ammesso che valga per il numero n, vale anche per n+1, allora P vale per qualunque numero n."
Giuseppe Peano, Arithmetices principia nova methodo exposita.
Va ricordato che egli presentò i suoi postulati esprimendosi in simboli, e non con le parole sopra riportate.
Qui il metodo assiomatico raggiunge un grado di precisione mai ottenuto prima, non lasciando adito ad alcuna ambiguità di significato.
Il lavoro di Peano comparve nel 1889, cioè l'anno successivo alla formulazione da parte di Dedekind di assiomi simili. A dispetto dell'impressionante somiglianza degli assiomi cui erano giunti, i risultati erano stati ottenuti indipendentemente (come non raramente succede).
Peano non poneva la sua indagine all'interno di un contesto insiemistico, ritenendo le nozioni di classe e insieme non meno elementari di quella di numero, che egli assumeva come concetto primitivo. Riuscì, grazie alla sua notazione, ad esprimere meglio la portata del fondamentale principio di induzione matematica.
Peano influenzò gli sviluppi successivi della logica simbolica e in particolare il filone logicista di Frege e Russell inteso a costruire la matematica sulle fondamenta della logica. L'opera di Peano deve essere tuttavia tenuta distinta da quella di Frege e Russell, perché Peano non voleva costruire la matematica sulle fondamenta della logica, che per lui era soltanto l'ancella della matematica.
Nell'ambito della Esposizione Internazionale di Parigi del 1900 si svolse all'inizio del mese di agosto il Congresso Internazionale di Filosofia. Fra i partecipanti c'erano il famoso e maturo Giuseppe Peano e il giovane e sconosciuto Bertrand Russell. Quando Peano parlò delle sue definizioni, Russell, come racconterà più tardi nell'autobiografia, ne rimase folgorato. Notò che Peano era sempre il più preciso e nelle discussioni riusciva facilmente ad avere la meglio. Russell gli chiese copie dei suoi pionieristici lavori e capì che il matematico torinese aveva trovato lo strumento di analisi che egli stesso stava cercando.
A partire dai suoi assiomi Peano stabilisce tutte le proprietà usuali dei numeri naturali. Dai naturali poi si possono definire e stabilire le proprietà degli interi negativi, dei numeri razionali ed infine degli irrazionali e quindi dei reali. Fu Hamilton a basare i numeri complessi su quelli reali. La base logica di questo approccio consiste in una qualche serie di asserzioni sui numeri naturali, come ad esempio gli assiomi di Peano, mentre tutti gli altri numeri vengono costruiti.
Hilbert lo chiamava metodo genetico e pur concedendo che può avere un valore pedagogico o euristico, riteneva più sicuro dal punto di vista logico applicare il metodo assiomatico direttamente all'intero sistema dei numeri reali.
Poincarè, che influenzò notevolmente gli intuizionisti, riteneva fondamentale il principio di induzione matematica che chiamava "ragionamento per ricorrenza. (Questa regola, inaccessibile alla dimostrazione analitica e alla esperienza è il vero tipo di giudizio sintetico a priori)". Esso non è basato sui principi d'identità e non contraddizione (giudizi analitici) né sull'esperienza (giudizi a posteriori), ma ha le potenzialità di una catena infinita di sillogismi.
Il principio d'induzione matematica, pur avendo qualche affinità con il ragionamento induttivo che si applica ad esempio in fisica è più sicuro poiché non richiede alcuna fiducia sull'uniformità della natura (vedi Hume).
Nelle aziende quando si devono stimare velocemente formule o indici relativi a problemi di ammortamento, interessi o più in generale valutazione degli investimenti si procede a controllare se il risultato è vero per diversi dati d'ingresso (ad esempio per un diverso numero di anni di vita presunta). Se il risultato delle verifiche è positivo in due o tre casi si assume (magari in prima battuta) la validità generale della formula sotto esame, cosa che un matematico giustamente non farebbe mai. Il principio d'induzione matematica fornisce una semplice, efficace soluzione a questi problemi perchè è al contempo rigoroso ma semplice (le verifiche devono essere fatte solo per 0, n ed n+1): esso può essere facilmente utilizzato anche da non matematici.