La previsione diviene impossibile e si ha un fenomeno fortuito [Poincaré]

"Una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancar di vedere, e allora diciamo che l'effetto è dovuto al caso. Se conoscessimo esattamente le leggi della natura e la situazione dell'universo all'istante iniziale, potremmo prevedere esattamente la situazione dello stesso universo in un istante successivo. Ma se pure accadesse che le leggi naturali non avessero più alcun segreto per noi, anche in tal caso potremmo conoscere la situazione iniziale solo approssimativamente. Se questo ci permettesse di prevedere la situazione successiva con la stessa approssimazione, non ci occorrerebbe di più e dovremmo dire che il fenomeno è stato previsto, che è governato da leggi. Ma non sempre è così; può accadere che piccole differenze nelle condizioni iniziali ne producano di grandissime nei fenomeni finali. Un piccolo errore nelle prime produce un errore enorme nei secondi. La previsione diviene impossibile e si ha un fenomeno fortuito". Henry Poincaré (1854, 1912): Les Méthodes nouvelles de la mécanique celeste
"In quel periodo partii da Caen, ove allora abitavo, per partecipare ad una escursione geologica organizzata dall'Ecole des Mines. Le peripezie del viaggio mi fecero dimenticare i miei lavori matematici; giunti che fummo a Coutances, salimmo in omnibus per non so quale gita. Nel momento stesso in cui misi piede sul predellino, ecco che mi venne l'idea, senza che nulla nei miei precedenti pensieri, almeno in apparenza, mi ci avesse predisposto. Le trasformazioni che avevo usato per definire le funzioni fuchsiane erano identiche a quelle della geometria euclidea. Non feci la verifica - non ne avrei avuto nemmeno il tempo, giacché appena seduto, ripresi la conversazione che avevo iniziato in precedenza - ma ne fui subito certo. Ritornato a Caen, verificai il risultato a mente fresca, per mettermi la coscienza a posto." Conferenza di Poincaré alla Societè de Psycologie.
Pierre Simon de Laplace (1749-1827) concepiva il determinismo come la possibilità di conoscere esattamente lo stato futuro di un sistema a partire dalla determinazione precisa del suo stato attuale. Nel suo Essai philosophique sur les probabilitiés scriveva: "Un intelligenza che, per un istante dato, potesse conoscere tutte le forze da cui la natura è animata, e la situazione rispettiva degli esseri che la compongono, e che inoltre fosse abbastanza grande da sottomettere questi dati all'analisi, abbraccerebbe nella stessa formula i movimenti dei più grandi corpi dell'universo e quelli dell'atomo più leggero: nulla le risulterebbe incerto, l'avvenire come il passato sarebbe presente ai suoi occhi. Lo spirito umano offre, nella perfezione che ha saputo dare all'astronomia, una debole parvenza di questa intelligenza".
In realtà (come intuì correttamente Poincaré e come e scritto nel suo primo pensiero riportato) il fenomeno della dipendenza forte dalle condizioni iniziali impedisce di prevedere lo stato futuro dei sistemi (anche di quelli non stocastici), contrariamente a ciò che riteneva Laplace. In effetti due sistemi che inizialmente presentano solo leggere differenze finiscono ben presto per non avere più niente in comune; pertanto i concetti di determinismo e di predicibilità debbono essere nettamente distinti.

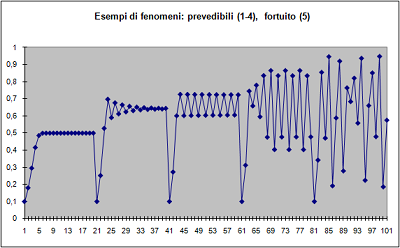
In figura sono riportati cinque andamenti generati da uno stesso sistema governato da una semplice applicazione logistica parametrica avente condizione iniziale 0.1: 1) il sistema converge rapidamente al valore 0.5, 2) il sistema converge più lentamente, e dopo diverse oscillazioni, al valore 0.65, 3) il sistema è diventato periodico. Dopo un rapido aggiustamento oscilla tra 0.60 e 0.72, 4) si ha uno sdoppiamento di periodo (0.40-0.83 e 0.48-0.88), 5) si ha un comportamento caotico il sistema è imprevedibile. Nel regime (5), quello caotico, variando solo di un miliardesimo la condizione iniziale, dopo qualche decina di iterazioni i valori trovati sono completamente diversi: il sistema è sempre deterministico, ma non predicibile.
Il secondo pensiero di Poincaré fa comprendere come matematica e psicologia (anche filosofia) siano fortemente connesse nelle attività di problem solving. In particolare si affronta il problema della scoperta matematica (razionalità o intuizione ?). Per Poincaré la scintilla determinante avviene con l'intuizione, poi segue la verifica razionale a conferma di quanto trovato. Oggi le neuroscienze, indagando le funzionalità del cervello, parlano di un sistema 1 intuitivo veloce e di un sistema 2 più lento, ma razionale. In Science e Méthode a proposito del ragionamento matematico e dell'intuizione Poincaré scrive: ".... che cos'è la creazione matematica? Essa non consiste nel produrre nuove combinazioni di entità matematiche già note; questa è cosa che chiunque potrebbe fare, ma le combinazioni così prodotte sarebbero in un numero infinito, e per lo più prive di ogni interesse. Creare consiste esattamente nel non produrre combinazioni inutili e nel produrre quelle che sono utili, e che sono una piccola minoranza. l'invenzione è discernimento, scelta." "Ho detto che inventare è scegliere; ma il termine, forse, non è completamente esatto. Esso fa pensare a un acquirente dinnanzi al quale si dispieghi un gran numero di esemplari e che li esamini uno dopo l'altro, per operare una scelta. Nel nostro caso gli esemplari sarebbero così numerosi che non basterebbe una vita intera, per esaminarli tutti. In realtà le cose non stanno così . Le combinazioni sterili neppure si presentano alla mente dell'inventore. Mai nel dominio della sua coscienza, si manifestano combinazioni che non siano davvero utili, salvo alcune che egli rigetta ma che hanno qualche apparenza di utilità. le cose procedono come se l'inventore fosse un esaminatore di secondo grado, incaricato di interrogare soltanto i candidati che hanno già superato un precedente esame".
Giancarlo Rota, un grande matematico italiano del secolo scorso tenne a Milano alcuni seminari diretti a filosofi, informatici e matematici soffermandosi in particolare sul rapporto tra la semplicità intuitiva e le complesse descrizioni formali. La sua tesi di fondo era così esplicitata: "la formalizzazione non contribuisce alla conoscenza. La conoscenza è portata dal capire problemi e soluzioni. Cioè dalla semplicità".