Variabili casuali
In molti fenomeni aleatori il risultato di un esperimento è una grandezza che assume valori che variano in modo casuale. Tale grandezza viene indicata come variabile aleatoria.
Più precisamente, si definisce variabile aleatoria o casuale una variabile che
può assumere valori diversi in dipendenza del verificarsi di eventi aleatori che costituiscono una partizione di un insieme universo U prefissato.
Una variabile casuale (o aleatoria) viene classificata in base al numero di valori che può assumere. Nel caso in cui i valori che una variabile può assumere siano in numero finito (o infinito numerabile) si tratta di una variabile discreta, se può assumere un qualsiasi valore in un intervallo continuo è detta variabile continua.
Distribuzione di probabilità discreta
Data una variabile aleatoria discreta X che può assumere i valori x1, x2, …, xN,. Si dice l’insieme dei valori delle rispettive probabilità p1, p2, …, pN, con la condizione che
è detto distribuzione discreta di probabilità.
La funzione P(xi) che permette di calcolare per ogni valore xi (i = 1, 2, …, N) la relativa probabilità pi dicesi funzione di distribuzione di probabilità, per la variabile casuale discreta X. Quindi la distribuzione di probabilità della variabile aleatoria X è definita dall’insieme dei valori xi e delle rispettive probabilità pi.

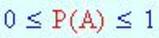





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo