vuoi
o PayPal
tutte le volte che vuoi
Monopolio od oligopolio? Questo è il problema. E' preferibile il primo oppure il secondo? Risposta unanime: " Né l'uno né l'altro. Vogliamo la libera concorrenza!" Tuttavia è noto che a rigore la libera concorrenza non esiste. Una buona approssimazione, secondo i testi di microeconomia, è data dai prodotti agricoli.
Ad esempio si suppone che la produzione di mele sia fatta da un numero grandissimo di piccoli/medi produttori nessuno dei quali ha dimensione e potere tali da imporre le proprie condizioni commerciali. In questo caso il prezzo è, o meglio sarebbe, stabilito dal mercato.
Tutti noi sappiamo che prezzo e quantità di un prodotto si formano, in linea di principio, dall'incontro di due curve: domanda (consumatori) e offerta (produttori).
Torniamo alla domanda iniziale: Monopolio o oligopolio?
In numerose situazioni ci sono motivi solidi e convincenti perché il numero dei produttori debba essere molto piccolo: 2, 3, 4 produttori. In questo caso si parla di Oligopolio (da oligo = poco, pochi). Il caso limite avviene quando il produttore è uno solo: monopolio (da mono = uno solo).
Oligopolio e monopolio avvengono per decisione dello Stato, che stabilisce per legge quanti produttori devono fornire un prodotto o servizio particolare. Oppure per motivi tecnologici: si tratta di un prodotto a tecnologia particolarmente innovativa che ha richiesto complesse/costose ricerche ed ha dato luogo a brevetti e/o know-how a protezione dei risultati per molti anni futuri. Conta anche la dimensione dell'investimento: in certi casi sono richiesti enormi capitali che poche società possono mettere insieme. Esempio di oligopolio: Boeing ed Airbus nel segmento grandi aerei.
E' piuttosto evidente che quando i produttori sono pochi, essi sono in grado di fare mercato. Ossia di avere notevole forza per influenzare il prezzo. La microeconomia ha lungamente studiato monopolio e oligopolio. La teoria del primo è ormai consolidata. Mentre l'oligopolio, che pure ha dato luogo a notevoli sviluppi applicativi, è ancora oggetto di studi, data la variabilità dei casi e dei possibili comportamenti competitivi. Di esso si occupa anche le Teoria dei Giochi.
Proviamo a sviluppare un esempio di monopolio/oligopolio.
Stati Uniti, far west, due grandi città in notevole espansione, distanti fra loro 110 miglia (circa 180 km). Le loro economie sono complementari. Entrambe possiedono importanti industrie e sono sedi di grandi società. In una di queste sono situati uffici governativi. Esiste un intenso traffico di persone nei due sensi: impiegati, operai, imprenditori, professionisti, commercianti, insegnanti, politici, lobbisti, ... tutti in auto.
Il turnpike (autostrada a pedaggio) che unisce le due metropoli è prossimo alla saturazione. Il Dipartimento Statale dei Trasporti è stato incaricato di proporre al Governatore una soluzione adeguata per i prossimi decenni. Si potrebbe costruire una nuova autostrada parallela a quella esistente, ma ciò aggraverebbe il problema dell'inquinamento, al quale è sensibile una vasta fetta dell'elettorato. Soluzione alternativa: una linea ferroviaria alta velocità che colleghi i due centri in 45 minuti, senza fermate intermedie.
Il Dipartimento dopo analisi accurate redige un progetto della nuova linea e decide di indire una gara per l'appalto e l'esercizio della stessa. Si invitano, su base federale, tutti i gruppi del settore a presentare una dichiarazione di interesse, corredata da un business plan preliminare.
Dopo alcuni mesi tre gruppi, attivi nel business ferroviario sulla costa dell'est, inviano la loro proposta. Ognuno propone di formare una società ad hoc, finanziata interamente con emissione di azioni che saranno quotate a Wall Street. Il dipartimento, dopo un attento esame delle dichiarazioni e ulteriori valutazioni, formula una serie di proposte alternative da sottoporre ai decisori.
Si potrebbe stabilire di affidare tutto il business a una sola società (monopolio) oppure a due o tre (oligopolio). In caso di oligopolio la linea ferroviaria potrebbe essere costruita in consorzio mentre il servizio ferroviario sarebbe gestito separatamente, in concorrenza (non certo perfetta).
Un primo passo fondamentale è cercare di capire la dimensione del mercato lato domanda. Per questo serve la curva di domanda. Essa esprime il legame tra la quantità q che i consumatori desiderano acquistare in funzione del prezzo p offerto dai produttori:
p = a - kq
In essa a e k sono due parametri positivi determinati per regressione.
E' dunque una retta a pendenza negativa. Tanto minore è il prezzo, tanto maggiore è la quantità che il consumatore comprerebbe. Si vede facilmente che: 0 < p < a , mentre: 0 < q < a/k.
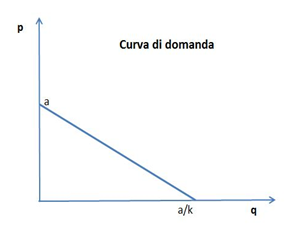
Nel caso in esame il Dipartimento, ha costruito la curva di domanda sulla base di dettagliate ricerche di mercato, ottenendo: a = 170 (USD/biglietto) , k = 4 (USD/biglietto/Mbiglietti). Dove p è il prezzo del biglietto one way (unidirezionale) espresso in dollari (USD/biglietto), mentre la quantità q è il numero(in milioni) di biglietti venduti in un anno. Notiamo incidentalmente che la ferrovia AV venderà un servizio (il trasporto del passeggero), non certo un prodotto.
Il Dipartimento ha calcolato che l'investimento totale (comprensivo della costruzione della linea AV completa della segnalazione, dell'acquisto del materiale rotabile e dei costi necessari alla costituzione della società, incluso il capitale circolante) sia 85 M USD/miglio (M sta per Mega = milioni).
La ferrovia è un business complesso ed economicamente rischioso, perciò lo Stato si rende disponibile a finanziare a fondo perduto metà dell'investimento.
DOMANDA 1. La prima alternativa considerata dal Dipartimento prevede che costruzione ed esercizio dalla linea AV sia data in monopolio al gruppo più solido ed importante dei tre, che costituirà una società denominata FASTRACK. Essa sarà creata emettendo azioni per creare il Capitale Sociale pari al 50% dell'investimento (mentre il restante 50% sarà erogato dalla Stato). Si stima che il Costo Marginale (MC) (il Costo Marginale è la derivata del costo rispetto alla quantità, nel nostro caso la derivata del Costo di esercizio annuo rispetto al numero di biglietti.) di esercizio del business di FASTRACK (incluso ammortamenti) sia di 58 USD/biglietto. In tal modo il Costo di esercizio è dato da:
C = MC*q
Facendo uso della Teoria del Monopolio trovare prezzo e quantità di monopolio che saranno, prevedibilmente, determinati e usati da FASTRACK. Calcolare anche Costo, Ricavo (il Ricavo è dato, ovviamente dal prodotto di prezzo e quantità: R = pq) e Risultato Economico lordo (Risultato Economico lordo, vale a dire ante imposte, EBT = R - C, EBT = Earning Before Tax) conseguiti dalla società.
Assumendo infine che il Risultato Economico lordo sia tassato con un'aliquota del 40% si determini l'Utile.
Infine ipotizzando che gli azionisti siano compensati con un dividendo annuo che, per semplicità, supponiamo sia esprimibile come interesse del 5,50% sul Capitale Sociale, determinare quanto ricevono (in totale) gli azionisti e quanto rimane disponibile come utile non distribuito.
DOMANDA 2. La seconda alternativa prevista dal Dipartimento prevede che si crei un oligopolio costituito da due società (FASTRACK e HSTRACK). In questo caso la linea AV sarà costruita in consorzio dividendo a metà l'investimento richiesto ai privati. In definitiva lo Stato metterà il 50%, mentre i due oligopolisti metteranno il 25% ciascuno. Si stima che i Costi Marginali siano diversi. Per FASTRACK assumere quello a DOMANDA 1, mentre per HSTRACK si stima MC = 61 USD/biglietto. Come si determina l'equilibrio di mercato nel caso del duopolio? Nella realtà esistono diverse teorie, ma il Dipartimento ritiene che la più aderente alla realtà, per questo tipo di oligopolio, sia quella di Cournot. Facendo uso della teoria di Cournot determinare il prezzo del biglietto (unico) di oligopolio, che sarà applicato da entrambe le società e la quantità (vale a dire il numero di biglietti) che ciascuna venderà. Anche in questo caso calcolare Ricavo, Costo, Risultato lordo, Utile. Assumendo che HSTRACK prometta di pagare agli azionisti un interesse del 5,75%, mentre FASTRACK paghi l'interesse di DOMANDA 1, determinare infine, per ciascuna società, quanto ricevono( in totale) gli azionisti e quanto rimane disponibile come Utile non distribuito.
DOMANDA 3. Infine il Dipartimento ha preso in considerazione l'alternativa, meno probabile, di un tripolio. Le società sarebbero FASTRACK, HSTRACK e SFTRACK. Il capitale sarebbe versato per il 50% dallo Stato, mentre il rimanente 50% sarebbe diviso in parti uguali fra i tre oligopolisti. Il Costo Marginale e l'interesse pagato agli azionisti sarebbero rispettivamente:
| Società | MC (biglietto) | Interesse agli azionisti |
| FASTRACK | 58 | 5,50% |
| HSTRACK | 61 | 5,75% |
| SFTRACK | 63 | 6,00% |
Applicando ancora la teoria di Cournot calcolare le stesse variabili di cui a DOMANDA 2.
Nota: i nomi delle tre società FASTRACK (binari veloci), HSTRACK (binari ad alta velocità), SFTRACK(binari super-veloci) sono di pura fantasia.
Notiamo incidentalmente che la ferrovia AV venderà un servizio (il trasporto del passeggero), non
certo un prodotto.
Il Dipartimento ha calcolato che l'investimento totale (comprensivo della costruzione della linea AV
completa della segnalazione, dell'acquisto del materiale rotabile e dei costi necessari alla
costituzione della società, incluso il capitale circolante) sia 85 M$/miglio( M sta per mega =
milioni). La ferrovia è un business complesso ed economicamente rischioso, perciò lo Stato si rende
disponibile a finanziare a fondo perduto metà dell'investimento.
DOMANDA 1
La prima alternativa considerata dal Dipartimento prevede che costruzione ed esercizio dalla linea
AV sia data in monopolio al gruppo più solido ed importante dei tre, che costituirà una società
denominata FASTRACK. Essa sarà creata emettendo azioni per creare il Capitale Sociale pari al 50%
dell'investimento (mentre il restante 50% sarà erogato dalla Stato). Si stima che il Costo Marginale
(MC) (*) di esercizio del business di FASTRACK (incluso ammortamenti) sia di 58 $/biglietto. In
tal modo il Costo di esercizio è dato da: C = MC*q
Facendo uso della Teoria del Monopolio trovare prezzo e quantità di monopolio che saranno,
prevedibilmente, determinati e usati da FASTRACK. Calcolare anche Costo, Ricavo(**) e
Risultato Economico lordo (***) conseguiti dalla società. Assumendo infine che il Risultato
Economico lordo sia tassato con un’aliquota del 40% si determini l'Utile. Infine ipotizzando che gli
azionisti siano compensati con un dividendo annuo che, per semplicità, supponiamo sia esprimibile
come interesse del 5,50% sul Capitale Sociale, determinare quanto ricevono (in totale) gli azionisti
e quanto rimane disponibile come Utile non distribuito.
DOMANDA 2
La seconda alternativa prevista dal Dipartimento prevede che si crei un oligopolio costituito da
due società (FASTRACK e HSTRACK). In questo caso la linea AV sarà costruita in consorzio
dividendo a metà l'investimento richiesto ai privati. In definitiva lo Stato metterà il 50%, mentre i
due oligopolisti metteranno il 25% ciascuno. Si stima che i Costi Marginali siano diversi. Per
FASTRACK assumere quello a DOMANDA 1, mentre per HSTRACK si stima MC = 61 $/biglietto.
Come si determina l'equilibrio di mercato nel caso del duopolio? Nella realtà esistono diverse teorie,
ma il Dipartimento ritiene che la più aderente alla realtà, per questo tipo di oligopolio, sia quella di
Cournot.
Facendo uso della teoria di Cournot determinare il prezzo del biglietto (unico) di oligopolio, che
sarà applicato da entrambe le società e la quantità (vale a dire il numero di biglietti) che ciascuna
venderà.
Anche in questo caso calcolare Ricavo, Costo, Risultato lordo, Utile. Assumendo che HSTRACK
prometta di pagare agli azionisti un interesse del 5,75%, mentre FASTRACK paghi l'interesse di
DOMANDA 1, determinare infine, per ciascuna società, quanto ricevono( in totale) gli azionisti e
quanto rimane disponibile come Utile non distribuito.
DOMANDA 3
Infine il Dipartimento ha preso in considerazione l'alternativa - meno probabile - di un Tripolio. Le
società sarebbero FASTRACK, HSTRACK e SFTRACK. Il capitale sarebbe versato per il 50%
dallo Stato, mentre il rimanente 50% sarebbe diviso in parti uguali fra i tre oligopolisti.
Il Costo Marginale e l'interesse pagato agli azionisti sarebbero rispettivamente:
Società MC ($/biglietto) Interesse
agli
azionisti
FASTRACK 58 5,50%
HSTRACK 61 5,75%
SFTRACK 63 6,00%
Applicando ancora la teoria di Cournot calcolare le stesse variabili di cui a DOMANDA 2.
*) Il Costo Marginale è la derivata del costo rispetto alla quantità. Nel nostro caso la derivata del
Costo di esercizio annuo rispetto al numero di biglietti.
(**) Il Ricavo è dato, ovviamente dal prodotto di prezzo e quantità: R = pq
–
(***) Risultato Economico lordo( vale a dire ante imposte): EBT = R C
(EBT = Earning Before Tax)
Nota: i nomi delle tre società FASTRACK (binari veloci), HSTRACK (binari ad alta velocità),
SFTRACK(binari super-veloci) sono di pura fantasia
RISPOSTA 1
In caso di monopolio l'offerta dell'unico produttore coincide con l'intera offerta di mercato. Il
monopolista stabilisce il livello di produzione q tale da massimizzare il suo profitto.
Ecco come:
Le curva di domanda e di costo, ricavo sono date rispettivamente da:
–
p = a kq
C = MCq –
R = pq = (a kq)q
Il Risultato Economico lordo (EBT) è dato dalla differenza tra ricavo e costo:
2
– – – –
EBT = R C = (a kq)q MCq = (a MC)q - kq
Il suo massimo si determina cercando il massimo relativo rispetto alla quantità prodotta:
– –
dEBT/dq = a MC 2kq = 0
–
Quindi: q = (a MC)/(2k) (a)
è punto di stazionarietà.
2 2
Inoltre d EBT/dq = - 2k < 0
Pertanto la soluzione trovata è un massimo relativo.
.
Gli economisti ottengono il medesimo risultato in modo più elegante, definendo la variabile MR,
(Ricavo Marginale = derivata del ricavo rispetto alla quantità):
Tornando alla definizione di profitto, sopra riportata:
–
EBT = R C
Derivando il profitto rispetto alla quantità, per ricercare il suo massimo si ottiene:
–
dEBT/dq = MR MC = 0
Questo vuol dire che il massimo profitto si determina quando: MR = MC
vale a dire quando il ricavo marginale eguaglia il costo marginale.
–
Ma noi sappiamo che MR = dR/dq = d[(a kq)q]/dq = a-2kq
Dunque risulta: MR = a-2kq =MC
Eguagliando ricavo e costo marginale si ottiene di nuovo la equazione (a)
Infine il prezzo di monopolio si deduce dalla curva di Offerta:
– –
p = a kq = a - k (a MC)/(2k) = (a + MC)/2 (b)
In conclusione le equazioni (a) e (b) definiscono quantità e prezzo di monopolio.
I dettagli di calcolo ed i diagrammi, riferiti ai dati del monopolista FASTRAK, sono riportati nel file
EXCEL, SHEET MONOPOLISTA.
RISPOSTA 2
La Teoria del duopolio di Cournot si applica a situazioni in cui i due produttori hanno sostenuto
grandi investimenti per dotarsi degli impianti necessari e quindi sono abbastanza rigidi in merito al
livello di produzione q. Ognuno di loro cerca di manovrare nell'ambito dei limiti rispettivi di
produzione, al fine di ottimizzare il profitto(lordo). Il prezzo di duopolio è il risultato della strategia
di ottimizzazione che entrambi adottano indipendentemente. In conclusione si determinano due
quantità q e q ( la cui somma eguaglia la domanda totale di mercato) ed un prezzo solo p che sarà
1 2
applicato da entrambi i produttori.
Come si giunge a definire le quantità ed il prezzo nel duopolio di Cournot? In modo semplice: il
primo produttore cerca il massimo profitto in funzione della quantità q (che gli produce) per ogni
1
possibile livello di produzione q del produttore rivale. Il rivale si comporta in modo uguale e
2
simmetrico.
Si procede così: – – –
EBT = R C = pq MC q = (a kq)q - MC q
1 1 1 1 1 1 1 1 1
ma q = q1 + q2 è la quantità totale prodotta e richiesta dal mercato.
Dunque: –
EBT =[(a k(q + q )]q - MC q
1 1 2 1 1 1
Per determinare il profitto massimo del primo produttore non resta che azzerare la derivata parziale
del suo profitto rispetto alla quantità q da lui prodotta:
1
∂EBT /∂q – –
= kq + (a k(q + q ) - MC = 0
1 1 1 1 2 1
Dalla quale si ottiene: – –
q = (a MC kq )/2k (c)
1 1 2
Siamo sicuri che la quantità q così determinata individui davvero il profitto massimo? Prendiamo
1
la derivata seconda: 2 21
∂ /∂q –
EBT = 2k
1
che è certamente negativa. Dunque abbiamo un massimo.
La retta così ottenuta si chiama Curva di Reazione del primo produttore e definisce la sua
–
produzione ottimale ai fini del profitto - per ogni valore di produzione q del rivale.
2
Quest'ultimo si comporta in modo uguale rispetto al primo produttore. Abbiamo:
– –
EBT =[(a k(q + q )]q MC q
2 1 2 2 2 2
∂EBT /∂q – –
= kq2 + (a k(q + q ) - MC = 0
2 2 1 2 2
– –
q = (a MC kq )/2k (d)
2 2 1
che è la Curva di Reazione del secondo produttore rispetto al primo.
Per far modo che ciascun produttore ottenga il profitto massimo basta ora incrociare le due curve
(rette) di reazione (c) e (d). In termini matematici: risolvere il sistema costituito dalle due equazioni
lineari.
Si perviene, alla fine a:
–
q = (a 2MC +MC )/3k
1 1 2
–
q = (a 2MC + MC )/3k
2 2 1
–
E dunque: q = q + q = (2a MC -MC )/3k
1 2 1 2
Mentre il prezzo(unico) di mercato si determina tramite la curva di domanda:
–
p = a - kq = a - (2a MC - MC )/3 = (a + MC + MC )/3
1 2 1 2
I dettagli di calcolo ed i diagrammi, riferiti ai dati di Domanda 2, sono riportati nel file EXCEL,
SHEET
RISPOSTA 3
In questo caso si considerano le tre società: FASTRAK, HSTRACK e SFTRACK. Ancora
assumiamo valido l'oligopolio di Cournot.
Il ragionamento fatto nel caso del duopolio si estende facilmente al caso del tripolio. In questo caso
si azzerano tre derivate parziali e si determinano tre curve di reazione.
Tralasciamo il procedimento un po' lungo e tedioso.
Si ottiene:
q = (a - 3MC + MC + MC )/(4k)
1 1 2 3
q = (a - 3MC + MC + MC )/(4k)
2 2 1 3
q = (a - 3MC + MC + MC )/(4k)
3 3 1 2
–
q = (3a - MC - MC MC )/(4k)
1 2 3 –
p = a - kq = a - (3a - MC - MC MC )/4 = (a + MC + MC + MC )/4
1 2 3 1 2 3
I dettagli di calcolo ed i diagrammi sono riportati nel file EXCEL, SHEET TRIPOLIO.
Mentre lo SHEET SOMMARIO E CONCLUSIONI confronta i risultati dei tre casi. Si vede
chiaramente che aumentando il numero di produttori il prezzo p scende e la quantità q aumenta: in
questo modo si avvantaggiano i consumatori (passeggeri) a detrimento dei produttori, e in definitiva
dei loro azionisti (alcuni dei quali potrebbero essere passeggeri). Questo può essere visto in termini
di numeri indice del prezzo del biglietto(lato consumatori) contro il numero indice dell'utile
complessivo delle società ferroviarie(lato produttori).
INDICI INDICE PREZZO
BIGLIETTI
MONOPOLIO INDICE UTILE
100 DUOPOLIO
90
UTILE
E 80
PREZZO 70
INDICI TRIPOLI
O
60 100 110 120 130 140 150
INDICE QUANTITA'
APPENDICE ALLE RISPOSTE
Il problema posto è stato risolto anche nel caso di un oligopolio fino a tre concorrenti. E' ben
difficile supporre che nella realtà una linea A








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









