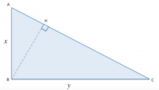
In un triangolo rettangolo ABC rettangolo in A il cateto AB è lungo 16cm, una delle due proiezioni dei cateti sull'ipotenusa supera l'altra proiezione di 2cm. Calcola perimetro e area del triangolo rettangolo.
Risoluzione
Ipotizziamo che il cateto[math]\widehat{AB}[/math]
, di 16 cm, sia il cateto maggiore; chiamiamo con [math]x[/math]
la proiezione sull'ipotenusa del cateto minore [math]\widehat{AC}[/math]
, mentre con [math]x+2[/math]
la proiezione del cateto maggiore [math]\widehat{AB}[/math]
.Possiamo sfruttare il primo teorema di Euclide, secondo il quale in un triangolo rettangolo un cateto è medio proporzionale fra l'ipotenusa e la sua proiezione sull'ipotenusa.
[math] \widehat{CB}: \widehat{AB} = \widehat{AB} : \widehat{HB}[/math]
Sapendo che
[math]\widehat{CB} = \widehat{CH} + \widehat{HB}[/math]
possiamo scrivere che
[math]\widehat{CB}= x + (x + 2) = x + x + 2 = 2x + 2[/math]
Sappiamo che il prodotto dei medi è uguale al prodotto degli estremi:
[math] \widehat{AB} \cdot \widehat{AB} = \widehat{CB} \cdot \widehat{HB}[/math]
[math]\widehat{AB} ^2 = \widehat{CB} \cdot \widehat{HB}[/math]
Sostituiamo e ricaviamo x dall'equazione:
[math] 16^2 = (2x + 2) \cdot (x + 2)[/math]
[math] 256 = 2x^2 + 4x + 2x + 4[/math]
[math] 2x^2 + 4x + 2x + 4 - 256 = 0[/math]
[math] 2x^2 + 6x - 252 = 0[/math]
[math] x^2 + 3x - 126 = 0[/math]
Troviamo le soluzioni usando la formula
[math] x = \frac{- b \widehat{A} \pm \sqrt{b^2 - 4ac}}{2a}[/math]
[math] x = \frac{- 3 \widehat{A} \pm \sqrt{3^2 - 4 \cdot (-126)}}{2} = [/math]
[math] x = \frac{- 3 \widehat{A} \pm \sqrt{9 + 504}}{2} = \frac{- 3 \widehat{A} \pm \sqrt{513}{2} [/math]
Possiamo portare fuori radice, sapendo che
[math] 513 = 9 \cdot 57 [/math]
[math] x = \frac{- 3 \widehat{A} \pm 3 \sqrt{57}}{2} \to [/math]
[math] x = \frac{-3 + 3 \sqrt{57}}{2} \text{e} x = \frac{- 3 - 3 \sqrt{57}}{2} [/math]
Sapendo che
[math]x[/math]
rappresenta la lunghezza di un segmento, essa non può essere negativa; dobbiamo quindi scartare la soluzione negativa e accettare solo [math]x = \frac{- 3 + 3 \sqrt{57}}{2}[/math]
.Calcoliamo quindi la lunghezza dell'ipotenusa
[math] \widehat{BC}[/math]
:
[math] \widehat{BC} = 2x + 2 = 2 \cdot \frac{- 3 + 3 \sqrt{57}}{2} + 2 = -3 + 3\sqrt{57} + 2 = -1 + 3\sqrt{57}[/math]
Con il teorema di Pitagora, determiniamo la lunghezza del cateto
[math] \widehat{AC}[/math]
:
[math]\widehat{AC} = \sqrt{\widehat{CB} ^2 - \widehat{AB}^2} = [/math]
[math] = \sqrt{(-1 + 3\sqrt{57})^2 - 16^2} = [/math]
[math] = \sqrt{(1 + 513 - 6\sqrt{57} - 256)} = [/math]
[math] = \sqrt{(258 - 6\sqrt{57})} [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
