Una superficie di rotazione intorno all'asse z è definita da una equazione del tipo ![]() Poniamo
Poniamo ![]() e consideriamo la funzione
e consideriamo la funzione
La rotazione di tale funzione intorno al proprio asintoto genera una superficie detta PSEUDOSFERA
La sua curvatura meridiana è quella della linea meridiana e vale
La sua curvatura parallela è quella della linea parallela e vale
Per la nostra funzione si ha
Il loro prodotto vale, in valore assoluto
Ma per i punti della pseudosfera , essendo tutti iperbolici, le due curvature hanno segno contrario, quindi la curvatura totale risulta negativa. Se assumiamo R come parametro,che chiamiamo k, avremo una superficie parametrica variabile al variare di k con curvature principali variabili ma, per ogni superficie, la curvatura totale sarà costante per ogni punto della superficie. Per vedere l'animazione cliccate sul grafico seguente, che è stato ottenuto per k=5 e considerando solo il ramo superiore.
Contenuto originale e autentico, validato dal Team di Esperti di Skuola.net



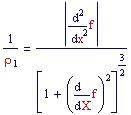
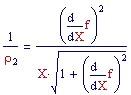
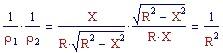






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo