Determinare il perimetro del triangoloavente per vertici i seguenti punti:
[math]A(1;0); B(-1;1); C(0;-2)[/math]
Svolgimento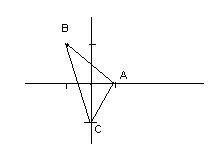
Per perimetro si intende la somma dei segmenti
[math]ar(AB), ar(BC), ar(AC)[/math]
.
Quindi calcoliamo le misure dei seguenti segmenti:
[math]ar(AB)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt((-1-1)^2+(1-0)^2)=\sqrt(4+1)=\sqrt5[/math]
[math]ar(AC)=\sqrt{(x_3-x_1)^2+(y_3-y_1)^2}=\sqrt((0-1)^2+(-2-0)^2)=\sqrt(1+4)=\sqrt5[/math]
[math]ar(BC)=\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}=\sqrt((0+1)^2+(-2-1)^2)=\sqrt(1+9)=\sqrt(10)[/math]
Pertanto
[math]2p=ar(AB)+ar(BC)+ar(AC)=\sqrt5+\sqrt5+\sqrt{10}=2\sqrt5+\sqrt{10}=\sqrt5(2+\sqrt2)[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
