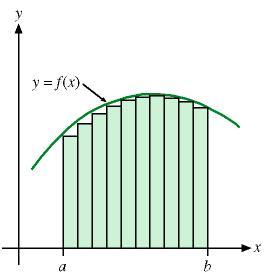
Per stimare l'area tra l'asse x e il grafico di una funzione non negativa f(x) in un intervallo [a, b], definiamo una partizione di [a, b] scegliendo n–1 punti x 1 , x 2 , . . ., x n –1 in [a, b], a = x 0 x 1 . . . x n –1 b = x n . Su ciascun subintervallo [x k –1 , x k ] costruiamo un rettangolo di larghezza Dx k = x k – x k –1 di altezza rispetto all'asse x uguale a f(c k ) . Il lato superiore di ciascun rettangolo deve toccare la curva in un punto (c k , f(c k )).
Sommando le aree di tutti i rettangoli, otteniamo un valore approssimato dell'area compresa tra l'asse x e f(x).
La somma
è chiamata somma di Riemann per f nell'intervallo [a, b].
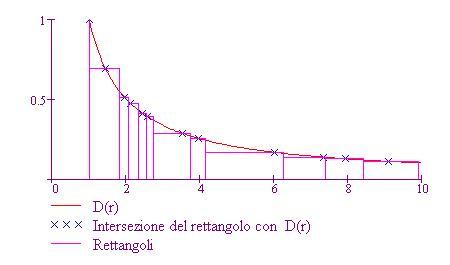
Trova una somma di Riemann per D(r) = 1/r nell'intervallo [1, 10].
Funzione:
Estremi dell'intervallo:
Numero di rettangoli:
Partizione:
Scegli un punto in ciascun subintervallo.
Calcola questa somma di Riemann.
Rappresentazione grafica:
Nota che diciamo di aver calcolato una somma di Riemann, piuttosto che la somma di Riemann. La somma dipende dalla partizione e dalla scelta dei punti c k in cui si valuta D(r).
Come ci si può aspettare, aumentando il numero dei rettangoli in una somma di Riemann si ottiene un valore approssimato con maggior precisione dell'area. Comunque, questo è vero solo se l'ampiezza del rettangolo più largo della partizione, chiamata norma della partizione, diventa sempre più piccola ossia tende a zero.
Nel precedente esempio, la norma è:
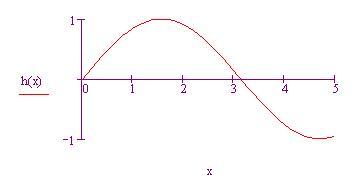
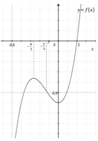
Stima l'area tra la curva e l'asse x tra gli estremi x = 0 e x = 5.
La funzione h(x)non è sempre positiva tra x = 0 e x = 5.
Per trovare l'area richiesta, dividiamo la somma di Riemann in più parti.
h(x) è non negativa in [0, p ] e negativa in ( p , 5]. Costruiamo due somme di Riemann, la prima sommando le aree dei rettangoli nella partizione di [0, p ] e la seconda sommando le opposte delle aree dei rettangoli nella partizione di [ p , 5].
Prima partizione
Numero di rettangoli:
Estremi del primo intervallo:
Larghezza di ciascun rettangolo:
Usiamo l'estremo sinistro di ciascun subintervallo per definire i vari rettangoli.
Seconda partizione
Numero di rettangoli:
Estremi dell'intervallo:
Larghezza di ciascun rettangolo:
Usiamo l'estremo sinistro di ciascun subintervallo per definire i vari rettangoli.
L'area totale è:
Che cosa succede al valore dell'area sotto la curva se n viene incrementato?
Per saperlo e per vedere l'animazione clicca sul grafico seguente!
Animazione a cura di Carlo Elce

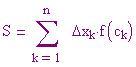
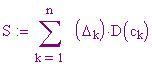
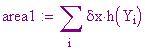
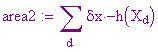
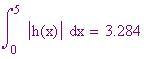





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo