Concetti Chiave
- Il libro di Osserman celebra l'immaginazione umana, sottolineando come la matematica sia essenziale per comprendere la struttura nascosta dell'universo.
- La matematica è paragonata a una lingua che, una volta appresa, rivela la bellezza e il fascino delle leggi fisiche che governano il cosmo.
- Osserman descrive come filosofi-scienziati dell'antica Grecia utilizzassero la matematica per esplorare il mondo, evidenziando la misura della Terra da parte di Eratostene.
- Il libro esplora come le scoperte di geometria differenziale e geometrie non euclidee abbiano rivoluzionato la comprensione matematica dello spazio.
- Osserman integra discipline come matematica, fisica e astronomia, mostrando la loro interdipendenza nel contesto dell'esplorazione scientifica dell'universo.
Poesia dell'universo, l'esplorazione matematica del cosmo R. Osserman  Quale sia la poesia dell'universo di cui parla Ossermann lo si capisce da subito leggendo le citazioni che introducono il libro. "La matematica pura è, a modo suo, la poesia delle idee logiche." A. Einstein "Una dimostrazione eseguita con eleganza è una poesia sotto ogni aspetto, tranne che nella forma in cui è scritta." M. Kline "C'è una ricchezza d'immaginazione sorprendente nella matematica della natura, e Archimede ebbe almeno altrettanta immaginazione di Omero.
Quale sia la poesia dell'universo di cui parla Ossermann lo si capisce da subito leggendo le citazioni che introducono il libro. "La matematica pura è, a modo suo, la poesia delle idee logiche." A. Einstein "Una dimostrazione eseguita con eleganza è una poesia sotto ogni aspetto, tranne che nella forma in cui è scritta." M. Kline "C'è una ricchezza d'immaginazione sorprendente nella matematica della natura, e Archimede ebbe almeno altrettanta immaginazione di Omero.
Indice
Matematica e immaginazione
" Voltaire Tutto il libro, afferma lo stesso autore, è una celebrazione dell'immaginazione umana: "la capacità di compiere quel tipo di salti mentali senza i quali l'impatto del mondo esterno sui nostri sensi si ridurrebbe per la maggior parte a rumore. Immaginazione e immagini matematiche, strettamente unite, forniscono quella visione che ci permette di vedere la struttura nascosta ma mirabile sotto la superficie".
Esplorazione del cosmo e matematica
Osserman sembra convinto che l'esplorazione del cosmo avviene attraverso la ricerca della sua 'poesia interna' e cioè della matematica che lo descrive. "Studiare la matematica per capire le leggi della fisica non è diverso dall'imparare una lingua straniera quanto basta per cogliere qualcosa della speciale fragranza e bellezza della prosa o della poesia scritta in quella lingua. Nel corso di tale processo può benissimo capitare di essere affascinati dalla lingua stessa. Lo stesso vale per molte parti della matematica. Creato inizialmente per fornirci una conoscenza più profonda della natura del mondo che ci circonda, il linguaggio della matematica sviluppa la sua struttura e il suo ordine, una sua bellezza e un suo fascino.
Antiche osservazioni astronomiche
" L'inizio dell'esplorazione del mondo intorno a noi viene fatto risalire a più di duemila anni fa, quando i filosofi-scienziati dell'antica Grecia cercarono di determinare grandezza e forma della Terra. L'impresa non poteva che essere un'operazione di tipo matematico, poiché né i Greci né altre civiltà erano mai state in grado di esplorare realmente una parte rilevante del pianeta. Le prime osservazioni sono quelle relative alle eclissi di Luna, quando Sole, Terra e Luna si trovano perfettamente allineati e si può vedere l'ombra circolare della Terra spostarsi sul disco della Luna.
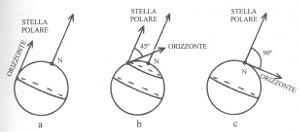 | Inoltre, ipotizzando un terra a forma di sfera, un osservatore posto all'equatore vedrebbe la stella polare esattamente sull'orizzonte, posto a una latitudine di 45° vedrebbe la stella polare a 45° sopra l'orizzonte, posto al polo nord vedrebbe la stella polare sulla propria testa. Tutto ciò in pieno accordo con il fatto facilmente osservabile secondo cui man mano che ci si sposta sulla superficie terrestre Le costellazioni appaiono sotto un angolo differente.
Misurazioni e rappresentazioni della Terra
|
Scoperte scientifiche e rappresentazioni
Un cambiamento significativo nel modo di rappresentarsi il mondo e nelle strutture matematiche che consentono di farlo si ha, nella prima metà dell'Ottocento, con la formulazione della geometria differenziale e delle cosiddette geometrie non euclidee. I principali artefici di questo cambiamento sono Gauss , Lobacevskij e Riemann . La geometria dello spazio curvo di Riemann fornisce gli strumenti indispensabili per proseguire l'esplorazione matematica dell'universo. Osserman si dimostra particolarmente abile nel rendere facilmente comprensibili complessi concetti della geometria differenziale e delle varietà riemanniane.
Scoperte fisiche e cosmologiche
La scoperta dell'elettricità da parte di Volta, delle onde elettromagnetiche da parte di Hertz, e ancora più sorprendente la scoperta dei raggi x, da parte di Roentgen, hanno consentito di estendere l'esplorazione fisica del mondo intorno a noi. L'astronomia ha avuto un grande sviluppo proprio a seguito della possibilità di esplorare le radiazioni invisibili all'occhio umano, la radiazione infrarossa, quella ultravioletta, i raggi x. Sulla base dello studio di queste nuove radiazioni, nel 1929 Hubble presenta le prove empiriche del fatto che l'universo potesse essere in espansione. A fianco a queste scoperte di natura sperimentale, altrettanto sconvolgenti sono state quelle teoriche dovute principalmente a Einstein, il quale ha fuso nella relatività ristretta e in quella generale lo spazio con il tempo.
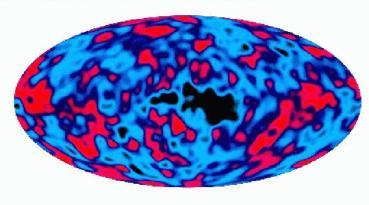 | Infine, nel 1992, viene realizzata una specie di 'foto istantanea' di quello che doveva essere l'universo nel momento in cui ebbe inizio lo spazio, si ratta della rappresentazione della radiazione cosmica di fondo che a partire dall'istante del big bang ha viaggiato nello spazio per giungere fino a noi.
Conclusione e interdisciplinarità
|
Domande da interrogazione
- Qual è il tema centrale del libro di R. Osserman?
- Come viene descritta la matematica nel contesto dell'esplorazione del cosmo?
- Quali sono alcuni dei momenti storici chiave nell'esplorazione della Terra menzionati nel libro?
- Quali scoperte scientifiche hanno ampliato l'esplorazione fisica del mondo?
- Qual è l'importanza della geometria differenziale e delle geometrie non euclidee nel libro?
Il tema centrale del libro è l'esplorazione matematica del cosmo, vista come una celebrazione dell'immaginazione umana e della poesia interna dell'universo, rappresentata dalla matematica.
La matematica è descritta come la poesia delle idee logiche e un linguaggio che, come una lingua straniera, permette di cogliere la bellezza e la struttura del mondo naturale.
Momenti chiave includono le misurazioni di Eratostene, il viaggio di Cristoforo Colombo e la scoperta delle Americhe, che hanno cambiato la rappresentazione del mondo.
Scoperte come l'elettricità di Volta, le onde elettromagnetiche di Hertz, i raggi x di Roentgen e le radiazioni invisibili hanno ampliato l'esplorazione fisica del mondo.
La geometria differenziale e le geometrie non euclidee, sviluppate da Gauss, Lobacevskij e Riemann, sono fondamentali per l'esplorazione matematica dell'universo e per comprendere lo spazio curvo.









 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo