Concetti Chiave
- Utilizza il software Cabri per costruire la retta di Eulero tramite una sequenza di strumenti, partendo dalla creazione di un triangolo.
- Costruisci le altezze, mediane e assi del triangolo per determinare ortocentro, baricentro e circocentro.
- Usa lo strumento "Retta" per tracciare una linea tra ortocentro e baricentro, verificando che il circocentro giaccia su questa retta.
- La retta di Eulero passa per ortocentro, baricentro e circocentro; nel triangolo rettangolo, questa coincide con una mediana.
- Muovendo i vertici del triangolo, puoi ottenere un triangolo equilatero dove i tre punti notevoli coincidono.
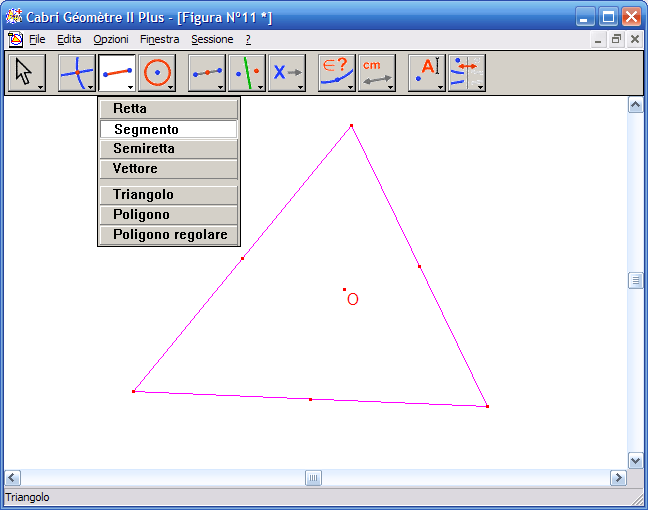
1. Dall'Icona n.3 (strumenti rettilinei) attiva lo strumento "Triangolo" e disegna il triangolo:
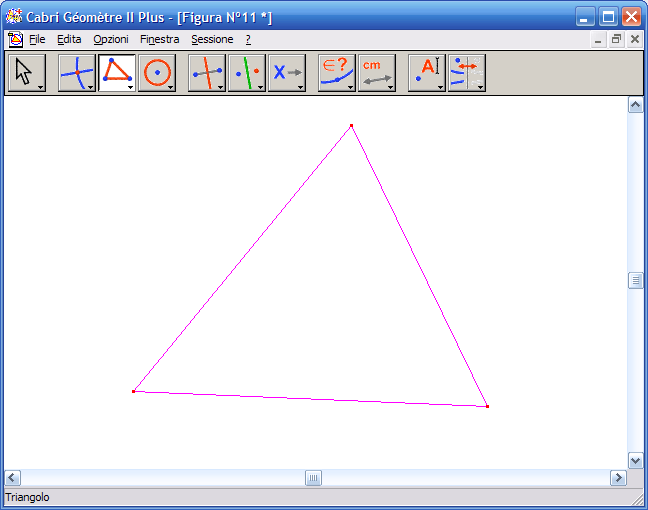
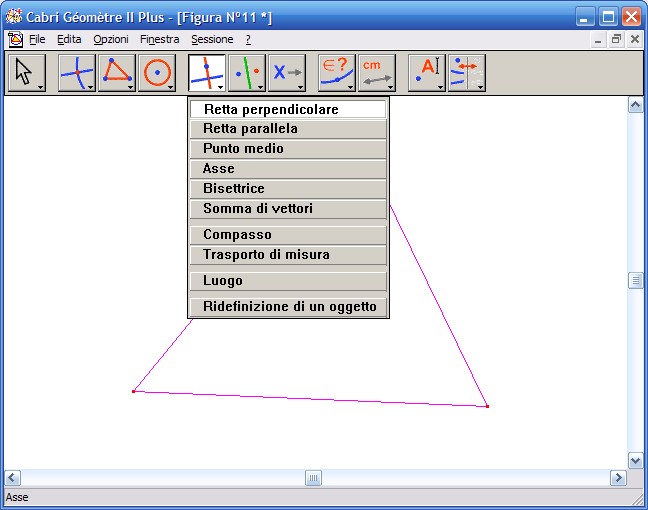
2. Dall'Icona n.5 (costruzioni) attiva lo strumento "Retta perpendicolare":
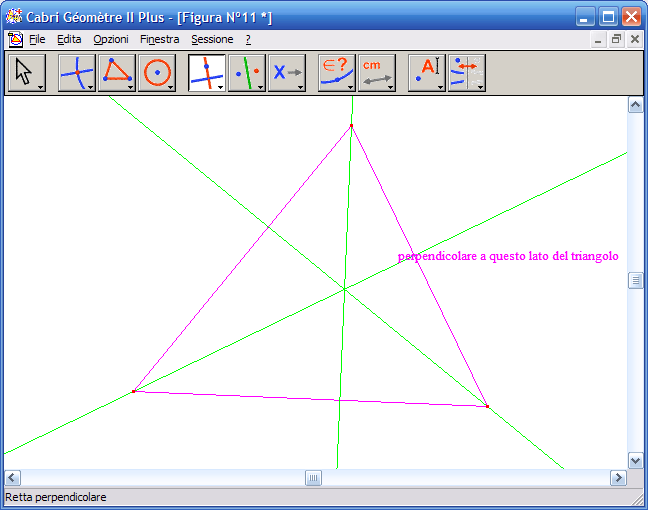
3. Fai clic su un vertice del triangolo e poi sul lato opposto, otterrai la retta dell'altezza del triangolo, ripeti l'operazione con gli altri vertici e le altre basi, otterrai le tre altezze del triangolo:
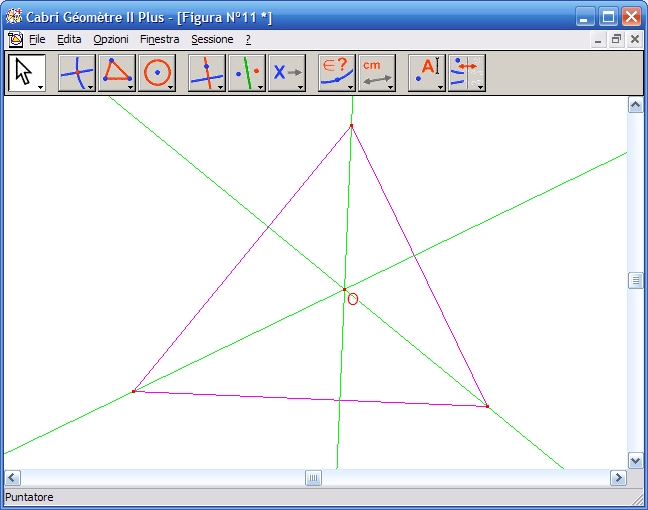
4. Dall'Icona n.2 (punti) attiva lo strumento "Punto di intersezione" e fai clic sul punto di intersezione delle altezze:
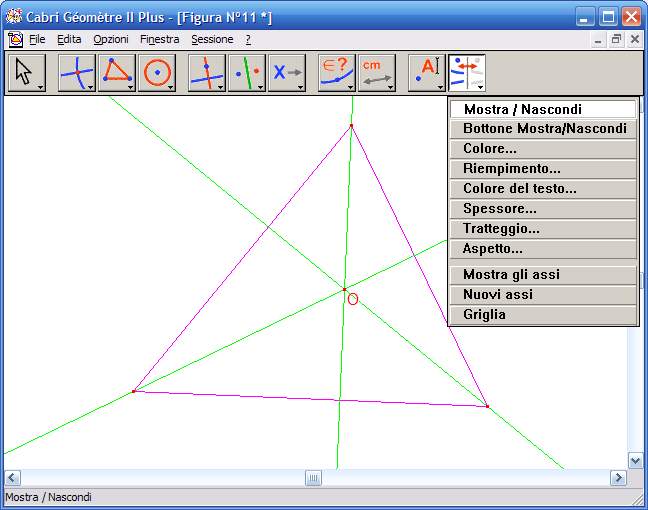
5. Dall'Icona n.11 attiva lo strumento "Mostra/Nascondi":
6. Fai clic sulle tre altezze per nasconderle dalla costruzione:
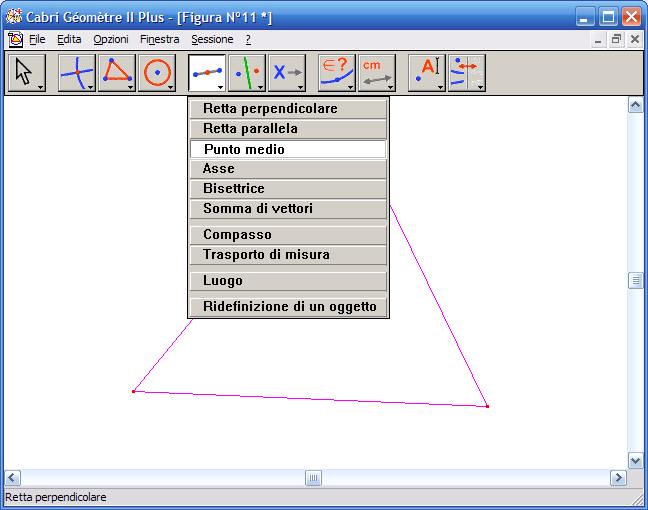
7. Dall'Icona n. 5 (costruzioni) attiva lo strumento "Punto medio":
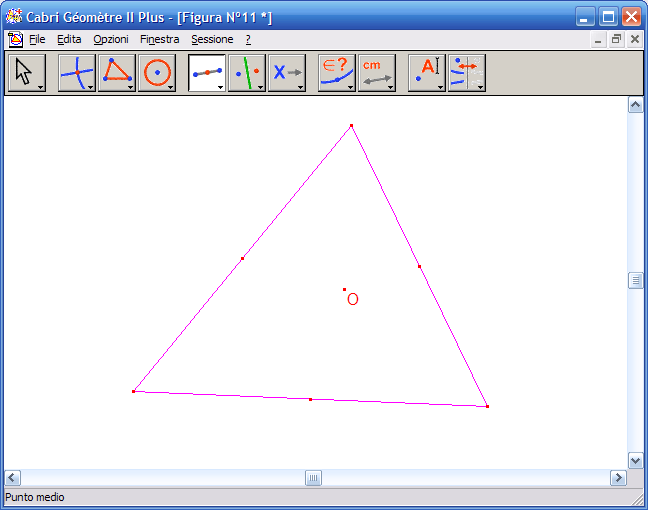
8. Con il mouse fai clic sui tre lati del triangolo per ottenere i rispettivi punti medi:
9. Dall'Icona n.3 seleziona lo strumento "Segmento":
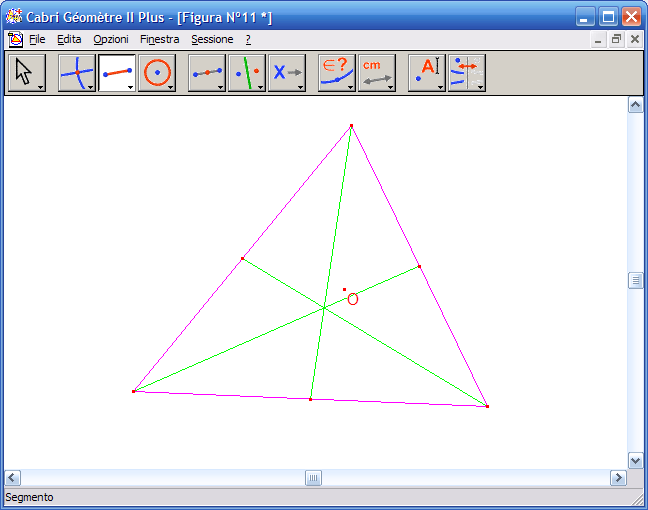
10. Fai clic su un vertice del triangolo e sul punto medio del lato opposto per ottenere la mediana; ripeti l'operazione con gli altri vertici:
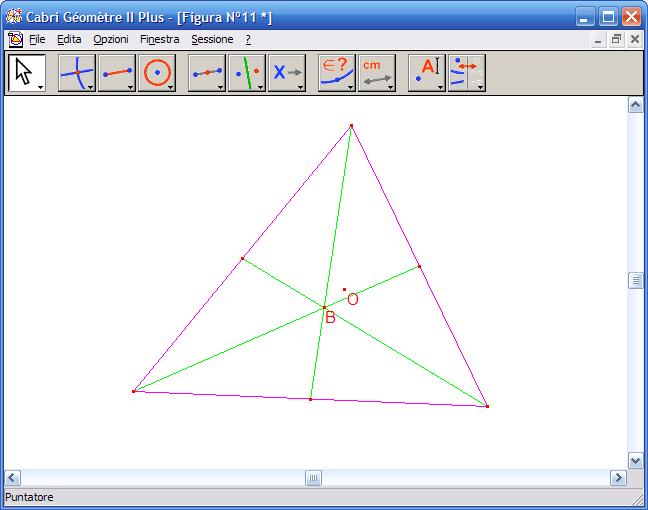
11. Dall'Icona n.2 attiva lo strumento "Punto di intersezione" e fai clic sul punto di intersezione delle tre mediane:
12. Attiva lo strumento "Mostra / Nascondi" e fai clic sulle mediane per nasconderle dalla costruzione:
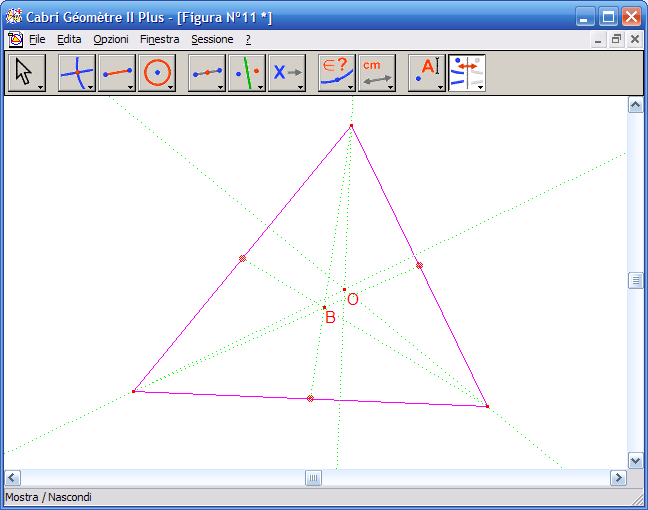
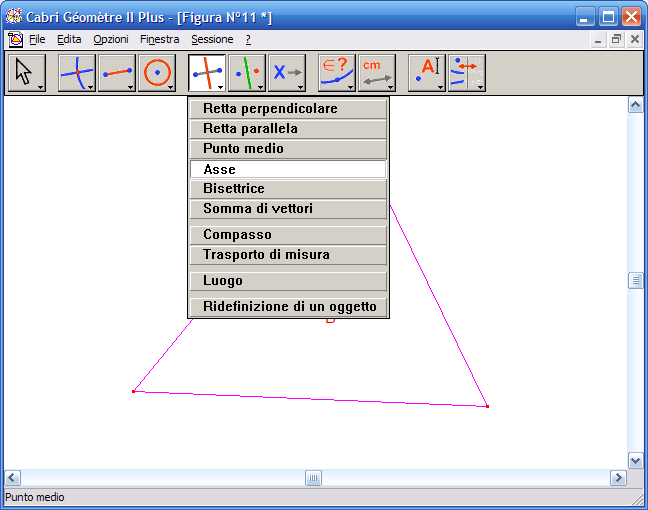
13. Dall'Icona n.5 attiva lo strumento "Asse":
14. Fai clic su ciascuno dei tre lati del triangolo per ottenere i tre assi:
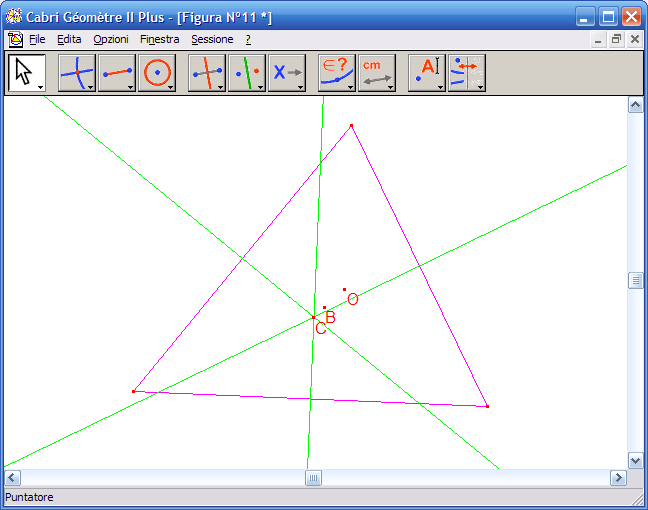
15. Con lo strumento "Punti di intersezione" fai clic sul punto di intersezione dei tre assi:
16. Con lo strumento "Mostra / Nascondi" fai clic su ciascuno dei tre assi per nasconderli dalla costruzione:
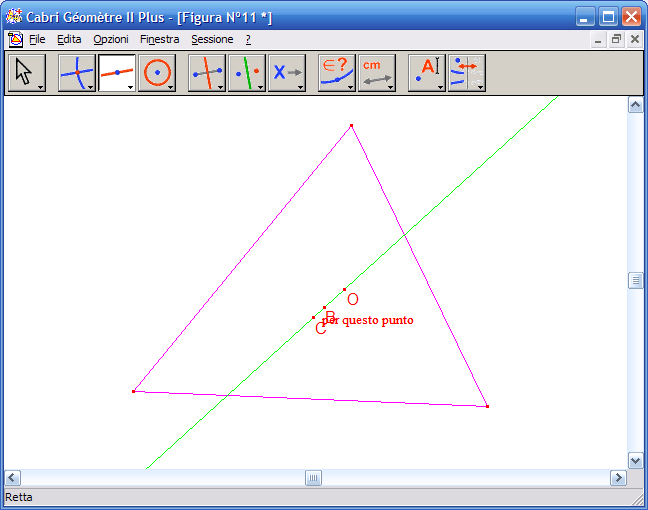
17. Dall'Icona n.3 attiva lo strumento "Retta" e fai clic su Ortocentro e Baricentro, otterrai la retta passante per questi due punti:
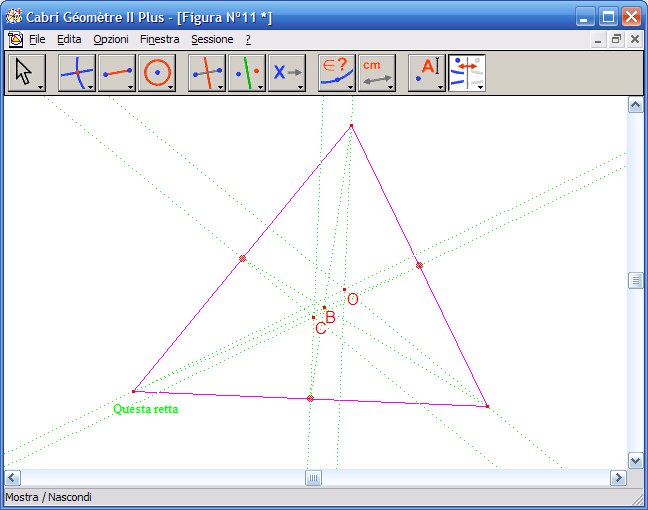
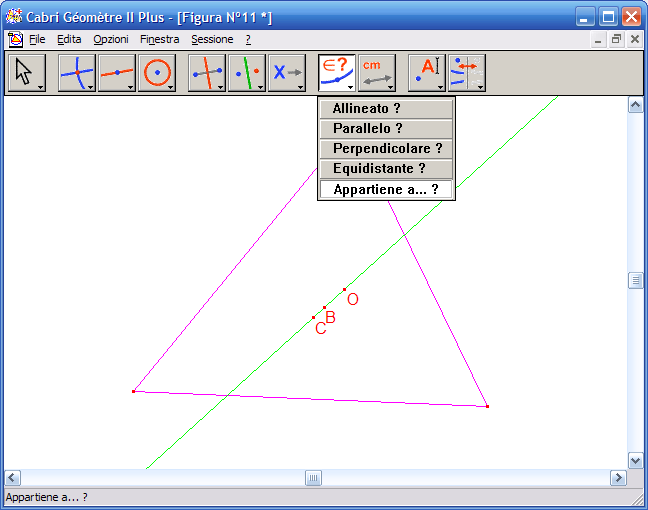
18. Dall'Icona n. 7 (relazioni) attiva lo strumento "Appartiene a...?":
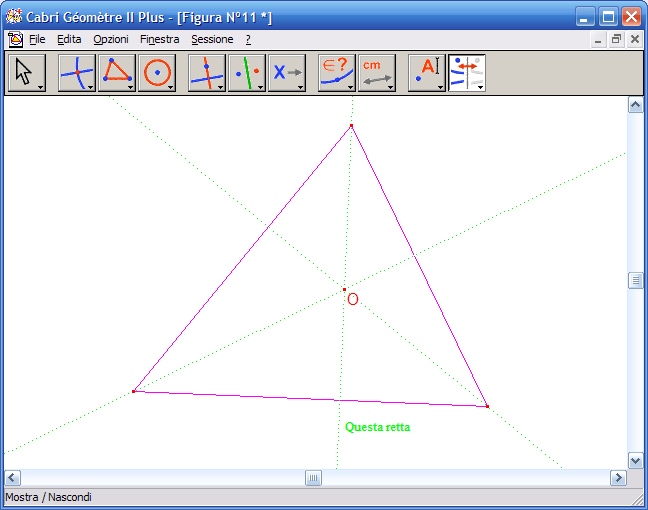
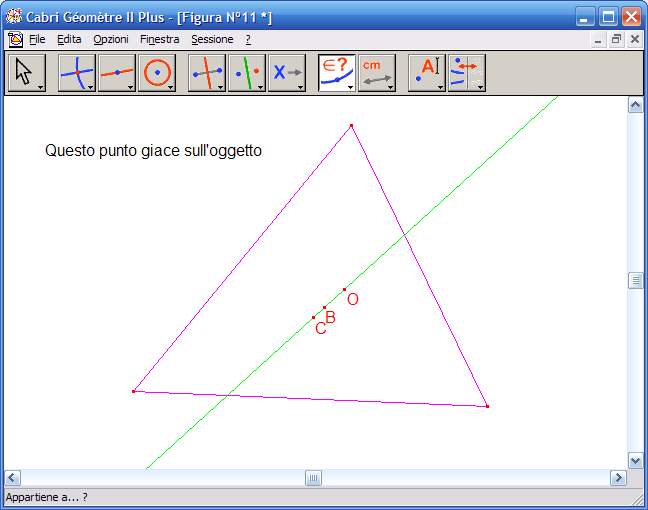
19. Fai clic sul Circocentro e poi per la retta precedentemente costruita, fai clic su un punto dell'area da disegno per avere la risposta, se la costruzione è corretta la risposta sarà: "Questo punto giace sull'oggetto". La retta costruita è quindi la retta che passa per ortocentro, baricentro, circocentro, nota con il nome retta di Eulero.
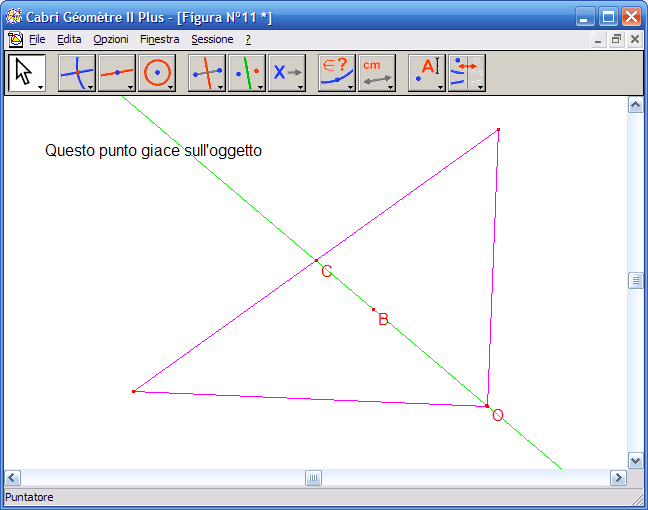
20. Con lo strumento "Puntatore" muovi uno dei vertici del triangolo fino a ottenere un triangolo rettangolo, noterai che l'ortocentro coincide con uno dei vertici del triangolo e la retta di Eulero coincide con la mediana.
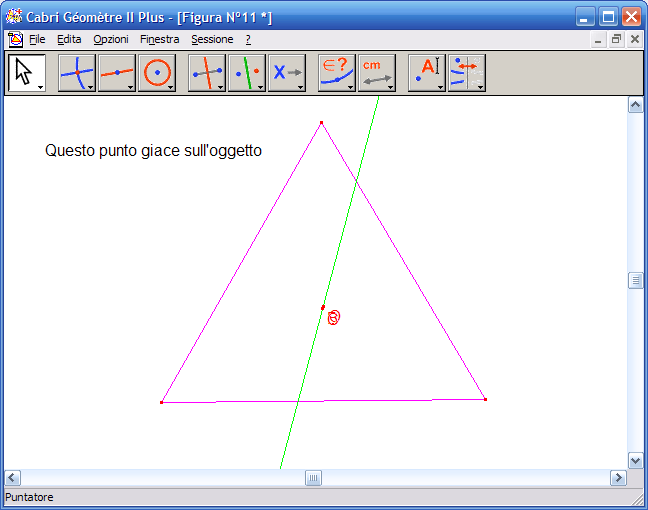
21. Continua a mouvere uno dei vertici del triangolo fino a fare in modo che i tre punti notevoli (ortocentro, baricentro e circocentro) coincidano, il triangolo ottenuto è un triangolo equilatero.
Domande da interrogazione
- Come si costruisce la retta di Eulero di un triangolo utilizzando il software Cabri?
- Qual è il ruolo del punto di intersezione delle altezze nella costruzione della retta di Eulero?
- Cosa accade alla retta di Eulero quando il triangolo diventa rettangolo?
- Come si verifica la correttezza della costruzione della retta di Eulero?
La costruzione della retta di Eulero inizia disegnando un triangolo, poi si tracciano le altezze, le mediane e gli assi del triangolo. Si identificano i punti di intersezione di queste linee per trovare l'ortocentro, il baricentro e il circocentro. Infine, si traccia una retta che passa per l'ortocentro e il baricentro, verificando che il circocentro giaccia su questa retta.
Il punto di intersezione delle altezze è l'ortocentro del triangolo, uno dei tre punti notevoli che, insieme al baricentro e al circocentro, giace sulla retta di Eulero.
Quando il triangolo diventa rettangolo, l'ortocentro coincide con uno dei vertici del triangolo e la retta di Eulero coincide con la mediana.
La correttezza della costruzione si verifica utilizzando lo strumento "Appartiene a...?" per controllare che il circocentro giaccia sulla retta costruita. Se la risposta è "Questo punto giace sull'oggetto", la costruzione è corretta.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo