Concetti Chiave
- Mathcad offre funzioni predefinite per calcolare media, mediana, deviazione standard e varianza di un insieme di dati.
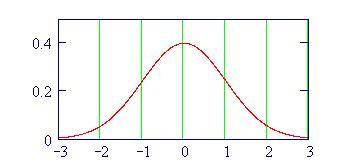
- Una distribuzione normale mostra dati concentrati attorno alla media con frequenza decrescente allontanandosi da essa, formando una curva a campana.
- In una distribuzione normale, circa il 68% dei dati cade entro una deviazione standard dalla media, il 95% entro due, e il 99.7% entro tre.
- I punteggi del test di Scienze della Terra vengono ordinati e analizzati per calcolare media, mediana e deviazione standard.
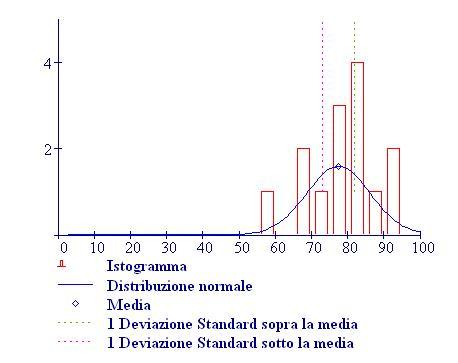
- Un istogramma dei punteggi confrontato con una distribuzione normale aiuta a visualizzare la distribuzione effettiva dei dati.
Dati:
Intervalli:
Per costruire l'istogramma digitiamo le istruzioni seguenti:
Numero di elementi nel vettore dei dati:
Valore medio dei dati:
Deviazione Standard:
Funzione interpolatrice normale:
Secondo voi i punteggi del test sono normalmente distribuiti?
Analisi dei Dati : Analisi dei dati e distribuzione normale con Mathcad
(Carlo Elce)
Mathcad dispone di molte funzioni predefinite che misurano la tendenza centrale e la dispersione di un insieme di dati. Usando queste funzioni possiamo trovare media, mediana, deviazione standard e varianza di un insieme di dati.
Una delle distribuzioni classiche che descrivono molti tipi di dati che ricorrono in natura, nelle scienze e altri campi la distribuzione normale. Quando dei dati sono normalmente distribuiti, tendono ad accumularsi intorno ad un valore centrale, la media, con i punti esterni a tale intorno che diventano tanto meno frequenti quanto pi sono lontani dalla media. Quando si rappresentano dati normalmente distribuiti, il loro grafico la cosiddetta curva a campana. Il punto massimo della curva la media dei dati. Una distribuzione normale ha approssimativamente il 68% della sua distribuzione che cade entro una deviazione standard 1 dalla media; approssimativamente il 95% della distribuzione entro una deviazione standard 2 dalla media; e approssimativamente il 99.7% della distribuzione entro una deviazione standard 3 dalla media.
In un Test di Scienze della Terra, un insegnante ha registrato i seguenti punteggi nel suo registro: 75, 80, 91, 90, 66, 84, 85, 80, 59, 77, 75, 80, 72 e 67. Calcolare media, mediana e deviazione standard di questi punteggi.
Prima creiamo un vettore di dati:
Da notare che usiamo l'operatore matriciale di trasposizione (M T ) per visualizzare i dati in orizzontale.
Quindi, disponiamo i dati in ordine crescente con la funzione predefinita sort di Mathcad:
La media il valor medio dei dati, la somma di tutti i punteggi diviso il numero dei punteggi:
La mediana il numero in posizione centrale o il valor medio dei punteggi centrali quando i dati sono ordinati:
La deviazione standard misura la dispersione dei dati: un valore basso indica che i dati tendono ad accumularsi vicino al valore centrale, mentre un valore alto indica che i dati sono sparpagliati.
Mathcad possiede anche delle funzioni predefinite per trovare il valore massimo e il valore minimo nei dati e anche il numero dei dati.
Valore massimo:
Valore minimo:
Numero dei dati:
Qui sotto, i dati del test sono rappresentati graficamente con un istogramma confrontato con una distribuzione normale avente la stessa media e la stessa deviazione standard:
indice corrispondente al primo elemento del vettore dei dati
Domande da interrogazione
- Qual è la funzione di Mathcad nell'analisi dei dati?
- Come si determina se i dati sono distribuiti normalmente?
- Quali sono i passaggi per calcolare la media e la mediana dei punteggi del test?
- Cosa indica la deviazione standard nei dati del test?
Mathcad offre funzioni predefinite per misurare la tendenza centrale e la dispersione, come media, mediana, deviazione standard e varianza.
I dati sono normalmente distribuiti se si accumulano intorno alla media e seguono la curva a campana, con specifiche percentuali di dati entro 1, 2 e 3 deviazioni standard dalla media.
Per calcolare la media, si sommano tutti i punteggi e si divide per il numero totale. La mediana è il valore centrale quando i dati sono ordinati.
La deviazione standard misura la dispersione dei dati; un valore basso indica dati vicini alla media, mentre un valore alto indica dati più sparpagliati.

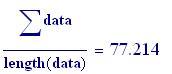





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo