Concetti Chiave
- Il trigger di Schmitt è un bistabile che alterna stati quando la tensione di ingresso supera soglie specifiche.
- La configurazione invertente del trigger di Schmitt impiega un amplificatore operazionale con formule specifiche per le soglie di tensione.
- Le tensioni di soglia [math]VT+[/math] e [math]VT-[/math] sono calcolate in base ai resistori e alla tensione di saturazione.
- Se la tensione di riferimento è diversa da zero, la transcaratteristica del circuito si sposta e cambia comportamento.
- Nelle equazioni, la tensione di soglia e le relative modifiche dipendono dalla tensione di riferimento e dai valori di resistenza.
Il trigger di Schmitt è un particolare squadratore d'onde, è un bistabile e passa da uno stato all'altro quando
Torna allo stato precedente quando
Il trigger di Schmitt viene in genere utilizzato per squadrare i segnali di varie forme d'onda e come rivelatore di soglia.
Visto che il trigger di Schmitt viene realizzato tramite l'utilizzo dell'amplificatore operazionale lo troviamo in due configurazioni quella invertente e quella non invertente.
Nella configurazione invertente abbiamo come formule note:
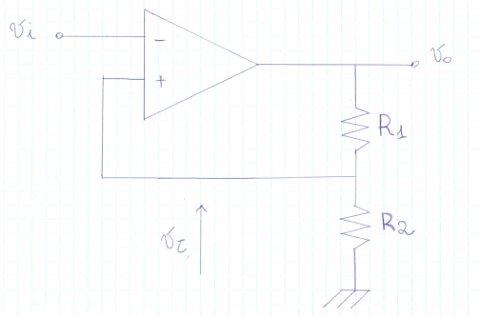
Quando
Se invece
Qui sotto è riportata la transcaratteristica della configurazione invertente, notiamo che è centrata perchè al circuito è collegata la massa.

Se invece la tensione di riferimento del trigger di Schmitt è diversa da zero
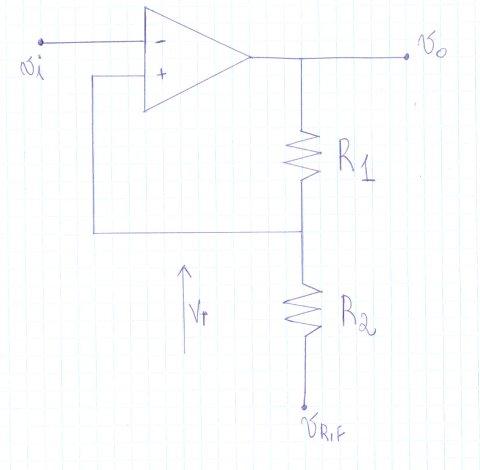
il primo con
Se invece
anche la transcaratteristica cambia, ed è spostata inoltre otteniamo:
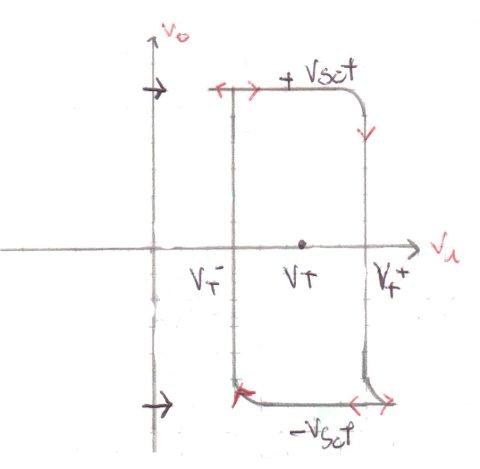







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo