
Soluzione del primo problema dello scientifico PNI.
a)
[math] g_1(x): x^2+y^2=4 \to y= \sqrt{4-x^2} [/math]
[math] g_2(x): (x-3)^2 + y^2= 1 \to y=- \sqrt{1- (x-3)^2} [/math]
[math] g_3(x): \(x- \frac92 \)^2 + y^2= \frac14 \to y= \sqrt{ \frac14- \(x- \frac92 \)^2} [/math]
per cui
[math] g(x)= \{ \sqrt{4-X^2} \ \ -2 \le x \le 2 \\ - \sqrt{-x^2+6x-8} \ \ 2 \le x \le 4 \\ \sqrt{-x^2+9x-20} \ \ 4 \le x \le 5 [/math]
i punti di non derivabilita' sono x=-2 , x=2, x=4 , x=5 in quanto si annullano gli argomenti delle radici
b)
essendo
[math] f'(x)=g(x) [/math]
si ha g(x)>0 per
[math] x \in (-2,2) \cup (4,5) [/math]
[math] g(x)>0 [/math]
per
[math] x=\{-2,2,4,5\} [/math]
si ha che
x=2 e' un massimo, x=4 e' un minimo
c)
[math] f(x)= \int_{-2}^{x} g(t) dt [/math]
[math] f(4)= \int_{-2}^4 g(t) dt = \int_{-2}^{2} g_1(t) + \int_{-2}^4 g_2(t) dt [/math]
che corrisponde a meta' dell'area della prima circonferenza da cui toglieremo meta' dell'area della seconda circonferenza, ovvero
[math] \frac42 \pi - \frac{\pi}{2}= \frac32 \pi [/math]
[math] f(1)= \int_{-2}^1 g(t) dt = \int_{-2}^0 g(t)dt + \int_0^1 g(t) dt [/math]
ovvero
1/4 area circ. 1 +
[math] \int_0^1 \sqrt{4-t^2} dt = \pi + \int_0^1 \sqrt{4-t^2}dt [/math]
Posto
[math] t=2 \sin \alpha [/math]
e dunque
[math] dt=2 \cos \alpha d \alpha [/math]
allora
[math] \sqrt{4-t^2}=2 \cos \alpha [/math]
[math] t=0 \to \alpha = 0 \\ t=1 \to \alpha= \frac{\pi}{6} [/math]
[math] = \pi + \int_0^{\frac{\pi}{6}}4 \cos^2 \alpha d \alpha = \\ = \pi \int_0^{\frac{\pi}{6}}2(1+ \cos 2 \alpha) d \alpha = \\ = \pi + \[2 \alpha + \sin 2 \alpha \]_0^{\frac{\pi}{6}}= \\ = \pi + \frac{\pi}{3}+ \frac{\sqrt3}{2}= \frac{3\pi}{4}+ \frac{\sqrt3}{2} [/math]
d)
[math] f'(x)=g(x) \\ f''(x)=g'(x)= \{ \frac{-x}{\sqrt{4-x^2}} \ \ -2>x>2 \\ \frac{x-3}{\sqrt{-x^2+6x-8}} 2>x>4 \\ \frac{-2x+9}{2 \sqrt{-x^2+9x-20}} \ \ 4>x>5 [/math]
[math] f''=0 \to x=0 [/math]
e siccome
[math]-2> x > 2[/math]
allora accettabile;
x=3 in
[math]2>x>4[/math]
, accettabile;
x=9/2 in
[math]4>x>5[/math]
, accettabile.
(Gli zeri della derivata seconda di f sono i punti di massimo e minimo di g(x) e quindi i punti di proiezione delle ascisse dei centri delle circonferenze.)
Per il grafico di f(x) si ha:
MAX in
[math] A \(2, f(2) \) \to A \(2, 2 \pi \) [/math]
MIN in
[math] B \(4, f(4) \) \to B \(4, \frac32 \pi \) [/math]
Flessi in
[math] F_1 (0, \pi) \ , \ F_2 \(3, \frac74 \pi \) \ , \ F_3 \( \frac92, \frac{25}{16} \pi \) [/math]
Inoltre
[math] f(5)= 2 \pi- \frac{\pi}{2} + \frac{\pi}{8} = \frac{13}{8} \pi [/math]
[math] f(-2)=0 [/math]
la funzione passa per
[math] C(-2,0) \ e \ D \(5, \frac{13}{8} \pi \) [/math]
Soluzione del secondo problema dello Scientifico PNI.
a)

[math] y^2=2x \ , \ x^2=y [/math]
[math] p_1:y^2=2x \\ F( \frac12,0) \\ d:x=- \frac12 [/math]
[math] p_2:y=x^2 \\ F(0, \frac14) \\ d:y=- \frac14 [/math]
[math] \{y^2=2x \\ y=x^2 [/math]
da cui
[math] x^4-2x=0 [/math]
e quindi
[math]x(x^3-2)=0 \to x=0 \to x= \sqrt[3]{2} [/math]
[math] A \( \sqrt[3]2 \ , \sqrt[3]{4} \) [/math]
b) il numero
[math] \sqrt[3]{2} [/math]
e' legato alla duplicazione del cubo.
Infatti se si ha un cubo di lato l e volume
[math] l^3 [/math]
se si considera un cubo di volume doppio, si avra'
[math]V=2l^3 [/math]
e quindi il lato del nuovo cubo rispetto al precedente sara'
[math] l_2=l \sqrt[3]{2} [/math]
Usiamo il metodo di Newton per il calcolo del valore approssimato.
Posto
[math] x= \sqrt[3]{2} \to x^3=2 \to x^3-2=0 [/math]
[math] f(x)= x^3-2 [/math]
abbiamo
[math] x_{(n+1)}= x_n- \frac{f(x)}{f'(x)} [/math]
E dunque
[math] x_{(n+1)}=x_n- \frac{x_n^3-2}{3x_n^2} [/math]
Posto
[math] x_0=1 [/math]
essendo
[math] 1> \sqrt[3]{2}>2 [/math]
Allora
[math] x_1=1- \frac{-1}{3}= \frac43 \approx 1, \bar{3} [/math]
[math] x_2=\frac43- \frac{\frac{64}{27}-2}{\frac{16}{3}}= \frac43- \frac{5}{72}= \frac{91}{72} \approx 1,263 \bar{8} [/math]
[math] x_3= \frac{91}{72}- \frac{ \( \frac{91}{72} \)^3-2}{3 \cdot \( \frac{91}{72} \)^2} \approx 1,2599 [/math]
[math] x_4= 1,2599 - \frac{(1,2599)^3-2}{3 \cdot (1,2599)^2} = 1,2599 [/math]
[math] \sqrt[3]{2}=1,2599 [/math]
c)

[math] C: \{y=k \\ y=x^2 [/math]
[math] \to C(\sqrt{k},k) [/math]
e
[math] B: \{y=k \\ y^2=2x [/math]
[math] B(k^2/2, k) [/math]
[math] \bar{BC}= \sqrt{(\sqrt{k}-k^2/2)^2+(k-k\)^2}= |\sqrt{k}-k^2/2|=g(k) [/math]
Ora
[math] \sqrt{k}-k^2/2 \ge 0 [/math]
da cui posto
[math] t= \sqrt{k}\to 2t-t^4 \ge 0 [/math]
[math] t(2-t^3) \ge 0 \to 0\le t \le \sqrt[3]{2} [/math]
quindi
[math]\sqrt{k}\le \sqrt[3]{2}\to k\le\sqrt[3]{4}[/math]
e si ha l'argomento del valore assoluto sempre positivo e quindi
[math]g(k)=\sqrt{k}-\frac{k^2}{2}[/math]
e
[math] g'(k) = \frac{1}{2\sqrt{k}}-k=0 \to 1-2k\sqrt{k}=0 \to k^{3/2}=\frac{1}{2}\to k=\frac{1}{\sqrt[3]{4}}[/math]
d)
Le sezioni sono corone circolari. Per il volume si ha
[math] V_{p1}-V_{p2}= \\ = \pi \[ \int_0^{ \sqrt[3]{2}} 2x dx - \int_0^{\sqrt[3]{2}}x^4 dx \] = \\ = \pi \[ x^2- \frac{x^5}{5} \]_0^{ \sqrt[3]{2}} = \\ = \pi \[ \sqrt[3]{4} - \frac{ \sqrt[3]{32}}{5} \] = \pi \[ \frac{5 \sqrt[3]{4}-2 \sqrt[3]{4}}{5} \] = \frac35 \sqrt[3]{4} \pi [/math]
Risposte al questionario
1 )
[math] p(x)=a_nx^m+q(x) [/math]
dove q(x) e' un polinomio di grado n-1
Sia
[math] g_m(x)=x^m [/math]
allora (indichiamo con D la derivata e come apice evidenziamo il grado della derivata (1 sara' la derivata prima, k la derivata k-esima)
[math] D^k(g_m(x))= \{ \frac{m!}{(m-k)!} x^{(m-k)} \ \ k \le m \\ 0 \ \ k>m [/math]
Infatti per induzione
[math] D^1 (g_m(x))=mx^{(m-1)} [/math]
e
[math] \frac{m!}{(m-k)!}x^{(m-1)}= \frac{m (m-1)!}{(m-1)!}x^{(m-1)}=mx^{(m-1)} [/math]
Se e' vero per k
[math] D^{(k+1)}(g_m(x))=D\[D^k(g_m(x))\]= \\ = D \[ \frac{m!}{(m-k)!}x^{(m-k)} \] = \frac{m!}{(m-k)!} \cdot (m-k) \cdot x^{(m-k-1)} = \\ = \frac{m!}{(m-k-1)!} x^{(m-k-1)} [/math]
Inoltre banalmente
[math] D \[g_m(x)\]=0 [/math]
Allora sara' vero che
[math] D^n \[p(x) \]= a_n D^n \[x^n \] + D^n \[q(x) \] = \\ = a_n \cdot \frac{n!}{(n-n)!} x^{(n-n)} + 0 = a_n \cdot n! [/math]
2)
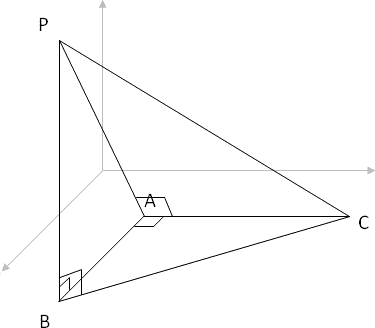
Gli angoli
[math] P \hat{B} A [/math]
e
[math] P \hat{B} C [/math]
sono rettangoli in B in quanto la retta r e' prependicolare al piano su cui giace il triangolo.
Per quanto riguarda
[math] P \hat{A}C [/math]
consideriamo il piano
[math] \pi [/math]
che contiene l'angolo
[math] P \hat{A} C [/math]
e la retta s su cui giace il segmento AC. La retta s e' perpendicolare al piano e pertanto dal momento che PA appartiene al piano, l'angolo in questione sara' anch'esso perpendicolare
3)
L'equazione della retta tangente al grafico di
[math]e^x[/math]
nel punto
[math](x_0;e^{x_0})[/math]
è
[math]y - f\left(x_0\right) = f'\left(x_0\right) \left(x - x_0\right)[/math]
[math]y - e^{x_0} = e^{x_0} \left(x - x_0\right)[/math]
[math]y = e^{x_0} x + e^{x_0} \left(1 - x_0\right)[/math]
Imporre il passaggio della retta per l'origine vuol dire imporre che il termine noto sia nullo, questo avviene in
[math]x_0 = 1[/math]
L'equazione della retta è dunque
[math]y = e x[/math]
, l'angolo formato con l'asse x è
[math]\alpha = \arctan (e) \approx 69.8^\circ[/math]
4 )
Cominciamo dal dimostrare che uno zero esiste. Banalmente
[math]\lim_{x\rightarrow \pm \infty} f(x)= \pm \infty[/math]
quindi dato che f(x) è continua esiste almeno uno zero esiste per il teorema dei valori intermedi. Essendo poi
[math]f'\left( x \right) = \frac{1}{3 \sqrt[3]{x^2} } + 3x^2 > 0[/math]
perché somma di quadrati, quindi la funzione è sempre crescente e lo zero è unico. Con il metodo delle tangenti
[math]x_{n+1} = x_n - \frac{ f\left( x_n \right) }{ f'\left( x_n \right) }[/math]
Iniziamo con
[math]x_0 = 1[/math]
[math]x_1 = 1 - \frac{ 1 }{ 3.333333333 } = {1 \over 4} = 0.25[/math]
[math]x_2 \approx 0.578010034092174[/math]
[math]x_3 \approx 0.56039934905323[/math]
[math]x_4 \approx 0.560088766594724[/math]
Dopo la quarta iterazione le prime due cifre restano uguali, quindi con l'approssimazione richiesta fa 0.56
5)
[math] g= \{ (x, f(x)) : x \in \mathbb{R} [/math]
Quindi G e' simmetrica rispetto a x=k, k appartenente a R
[math] P(x,f(x)) \\ Q(x',f'(x)) \\ x'=-x+2k \\ f(x')=f(x) \\ f(-x+2k)=f(x) [/math]
6)
[math]\left\{ \begin{matrix} x = 3 \cos t \\ y = 2 \sin t \end{matrix} \right.[/math]
con
[math]0 \le t > 2 \pi[/math]
Rappresenta un'ellissi, infatti elevando al quadrato, isolando le funzioni goniometriche e sommando abbiamo
[math]\left\{ \begin{matrix} x^2 = 9 \cos^2 t \\ y^2 = 4 \sin^2 t \end{matrix} \right. \\
\left\{ \begin{matrix} \frac{x^2}{9} = \cos^2 t \\ \frac{y^2}{2} = 4 \sin^2 t \end{matrix} \right.\\
\frac{x^2}{9} + \frac{y^2}{4} = 1[/math]
Questo rappresenta un'ellisse di semiassi a e b
7 )
Almeno una figlia è femmina, quindi i casi possibili sono MF, FM e FF
Il caso con 2 figlie femmine quindi è 1 su 3, quindi la probabilità è 1/3
8 )
ricordiamo che
[math] \( \begin{array}{c} n \\ \\ k \end{array} \)= \frac{n!}{k!(n-k)!} [/math]
Dal momento che i tre valori sono in progressione aritmetica, dovra' essere costante la differenza tra due elemnti consecutivi, e quindi la differenza tra il terzo elemento e il secondo dovra' essere uguale alla differenza tra il secondo e il primo.
Posto n>3, dal momento che la serie prevede n-3, avremo dunque
[math] \( \begin{array}{c} n \\ \\ n-3 \end{array} \) - \( \begin{array}{c} n \\ \\ n-2 \end{array} \) = \( \begin{array}{c} n \\ \\ n-2 \end{array} \) - \( \begin{array}{c} n \\ \\ n-1 \end{array} \) [/math]
E dunque
[math] \( \begin{array}{c} n \\ \\ n-3 \end{array} \) = 2 \( \begin{array}{c} n \\ \\ n-2 \end{array} \) - \( \begin{array}{c} n \\ \\ n-1 \end{array} \) [/math]
Da cui sviluppando i binomi:
[math] \frac{n!}{(n-3)!(n-(n-3))!} = 2 \frac{n!}{(n-2)!(n-(n-2))!} - \frac{n!}{(n-1)!(n-(n-1))!} [/math]
[math] \frac{n!}{3!(n-3)!}= \frac{\no{2}n!}{\no{2!}(n-2)!}- \frac{n!}{1(n-1)!} [/math]
Ricordando che n!=n(n-1)(n-2)(n-3)!
[math] \frac{n!}{6(n-3)!}= \frac{n!}{(n-2)(n-3)!}- \frac{n!}{(n-1)(n-2)(n-3)!} [/math]
Minimo comune multiplo e semplificazione del denominatore
[math] n!(n-2)(n-1)=6n!(n-1)-6n! [/math]
semplifichiamo n!
[math] (n-2)(n-1)=6(n-2) \to n-1=6 \to n=7 [/math]
Accettabile perche' >3
9 )

Disegnamo il segmento AB e la retta su cui giace BC in modo che l'angolo ABC sia di 45°. La distanza di A dalla retta è
[math]\frac{3}{\sqrt{2}} > 2[/math]
. Dato che la distanza è il segmento più breve che unisce un punto ad una retta, e che AC dato è minore della distanza, il triangolo non può esistere.

Per il secondo triangolo la distanza viene 3/2, quindi il segmento AC è maggiore. Chiamiamo H il piede della distanza sulla retta su cui giace BC. Possono esistere due triangoli, uno con il punto C tra A e H e uno sulla semiretta uscente da H non contenente A (infatti, facendo spostare il punto C sulla retta di BC, si ottengono con continuità segmenti AC di lunghezza compresa tra 3/2 e 3 nel segmento AH e maggiore di 3/2 sulla semiretta)
10 )
Nessuno di questi. Infatti si ha:
a:
[math]\pi \int_0^4 \left(\sqrt{x}\right)^2 dx = \pi \int_0^4 x^2 dx[/math]
b:
[math]\pi \int_0^{16} \left(y^2\right)^2 dy = \pi \int_0^{16} y^4 dy[/math]
c:
[math]\frac{\pi}{2} \int_0^4 \left(\frac{\sqrt{x}}{2}\right)^2 dx = \frac{\pi}{8} \int_0^4 x dx[/math]








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo