Siano
[math] A = { x âZ | -10 ⤠x ⤠+1 } [/math]
, [math] B = { x âZ | -1 ⤠x ⤠+1 } [/math]
e [math] C = { x âZ | x > -5 } [/math]
; determina: [math]A â© C [/math]
, [math]B ⪠C [/math]
, [math]B - C [/math]
, [math](A ⩠B) ⪠C [/math]
Risoluzione
Consideriamo i seguenti insiemi:
[math] A = { x âZ | -10 ⤠x ⤠+1 } [/math]
[math] B = { x âZ | -1 ⤠x ⤠+1 } [/math]
[math] C = { x âZ | x > -5 } [/math]
;
Quesito 1
L'intersezione di due insiemi è l'insieme degli elementi appartenenti sia al primo insieme che al secondo.
[math]A â© C = { x âZ | -4 ⤠x ⤠+1 }[/math]
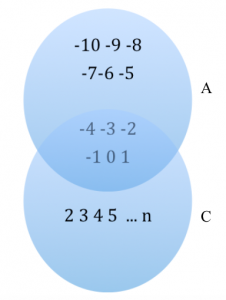
Quesito 2
L'unione di due insiemi è, invece, l'insieme di tutti gli elementi appartenenti al primo o al secondo insieme.Poiché B è un sottoinsieme di C, l'insieme derivato dall'unione di B con C consiste nell'insieme C stesso.
[math]B ⪠C = C = { x âZ | x > -5 } [/math]
;
Quesito 3
Per differenza di due insieme si intende l'insieme degli elementi del primo insieme che non appartengono al secondo.Poiché non vi sono elementi dell'insieme B che non appartengono all'insieme C ( B è un sottoinsieme di C ), la differenza di questi due insiemi sarà un insieme vuoto.
[math]B - C = â
[/math]
Quesito 4
Procediamo determinando prima l'intersezione fra l'insieme A e l'insieme B.Poiché l'insieme B è un sottoinsieme dell'insieme A, la loro intersezione sarà data dall'insieme B stesso.
[math]A â© B = B = { x âZ | -1 ⤠x ⤠+1 } [/math]
A questo punto, procediamo con l'unione con l'insieme C, che ci riporta all'esercizio precedente: poiché
[math] A â© B [/math]
è un sottoinsieme di C, l'insieme dato dall'unione di [math]A â© B[/math]
con C sarà l'insieme C stesso.
[math](A â© B) ⪠C = C = { x âZ | x > -5 }[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
