vuoi
o PayPal
tutte le volte che vuoi
Iperbole
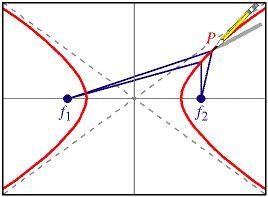
L'iperbole è l'insieme dei punti del piano tali che la differenza delle distanze da due punti fissi, detti fuochi, è costante.
In altre parole, la distanza del punto P sull'iperbole da f 1 meno la distanza di P da f 2 è una costante, s.
Poichè in un triangolo un lato è maggiore della differenza degli altri due la costante s (differenza tra Pf 1 e Pf 2 ) deve essere maggiore di zero, ma minore della distanza tra i due fuochi.
Centro:
Semiasse maggiore e semiasse minore:
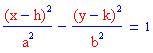
Iperbole orientata orizzontalmente:
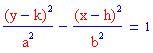
Iperbole orientata verticalmente:
Qui sotto sono stati disegnati i grafici di un'iperbole orizzontale e di una verticale. Puoi provare a cambiare le costanti a e b oppure clicca sui grafici seguenti!
Centro:
Costanti a e b:
Iperbole Orizzontale
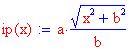
Per disegnare l'iperbole:
Per disegnare i fuochi:
Asintoti:
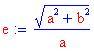
Eccentricità:
Iperbole verticale
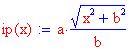
Per disegnare l'iperbole:
Per determinare i fuochi:
Asintoti:
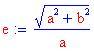
Eccentricità:
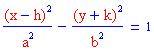
L'equazione
si espande in
Trova i valori di h, k, a, e b della seguente equazione:
Avrai ormai familiarità con i metodi visti precedentemente per risolvere un problema come questo. Se non ci riesci clicca qui!
L’IPERBOLE
Definizione: l’Iperbole è il luogo geometrico dei punti del piano per i quali la differenza
delle distanze da due punti fissi detti fuochi è costante.
Dimostrazione:
| |
´ ´
− =2
PF PF a
2 1
´ ´ ´ ´ ´ ´ ´ ´
( )
− =2 > − =2 >
PF PF a se PF PF ; PF PF a se PF PF
1 2 1 2 2 1 2 1
√
´ 2 2
( ) ( )
= +
PF x−c y−O
1 √
´ 2 2
( ) ( )
= +c +
PF x y−O
2
Quindi: √ √
2 2
2 2
sostituiamo nella equazione iniziale: ( ) ( )
−c + − +c + =2
x y x y a
√ √
2 2 2 2 2 2
sviluppiamo i quadrati sotto radice: +c −2 + =2 +c +
x cx y a+ x 2 cx+ y
eleviamo tutto alla seconda:
√
2 2 2 2 2 2 2 2 2 2
+ −2 =4 + +c + + + +2 +
x c cx+ y a x 2 cx+ y 4 a x c cx y
√
2 2 2 2
semplifichiamo i termini uguali: −4 −4 =4 +c +2
cx a a x cx+ y
√
2 2 2 2
dividiamo per -4: +a =−a +c + +
cx x 2cx y
4 2 2 2 2 2 2 2 2 2 2
eleviamo tutto alla seconda: + +2 + +2 +a
a c x a cx=a x a c a cx y
( ) ( )
2 2 2 2 2 2 2 2
semplifichiamo e raccogliamo: −a −a =a −a
c x y c
2 2 2 2 2 2
Essendo , lo possiamo sostituire con per semplificare, quindi
−a > −c =b
c 0 b a
2 2
. Sostituiamo e poi dividiamo per :
a b 2 2 2 2 2 2
−a =a
b x y b
2 2
x y ← EQUAZIONE DELL’IPERBOLE
− =1
2 2
a b
L’iperbole è una curva simmetrica rispetto all’asse delle x, rispetto all’asse delle y e
all’origine, O(0; 0). Infatti:
Simmetria asse x:
2
2 2 2
(− )
y
x x y
− =1, − =1
y →− y 2 2 2 2
a b a b
Simmetria asse y:
2 2 2 2
(−x ) y x y
− =1, − =1
x →−x 2 2 2 2
a b a b
Simmetria O(0; 0):
2 2
{ 2 2
(−x ) (− )
y x y
x →−x − =1, − =1
2 2 2 2
y →− y a b a b
Per disegnare un’ellissi servono due condizioni, perchè ci sono 2 costanti.
( )
2 2 2 2 2
+
x y b y a ( )
2 2 2 2 2
⇒ ⇒
=1+ =a = +
x x b y
2 2 2 2
a b b b
2
Poniamo :
x ≥ 0
2
a ( )
2 2
+
b y è di sicuro ≥ 0
2
b
Quindi la x esiste per ogni y
.
Seguiamo lo stesso procedimento per la y:
( )
2 2 2 2 2
−a
y x x b ( )
2 2 2 2 2
⇒ ⇒
= −1 =b = −a
y y x
2 2 2 2
b a a a
2
Poniamo :
y ≥ 0
2 2
b b
( ) ( )
2 2 2 2
⇒ ∪
−x −a ←a
a ≥ 0 è di sicuro ≥ 0 ; x ≥ 0 per x x> a
2 2
a a
Quindi la y non esiste se x è compresa tra –a e a .
Ora consideriamo l’equazione che rappresenta una coppia di rette passanti per l’origine
O(0; 0):
2 2
x y
− =0
2 2
a b
Man mano che ci si sposta verso valori più grandi, queste due rette si comportano come
l’iperbole. Questo avviene perchè aumentando i valori delle variabili x e y, il fattore 1
dopo l’uguale influisce sempre di meno e quindi le due equazioni, dell’iperbole e delle
due rette, tenderanno ad assumere gli stessi valori. Scomponendo l’equazione delle due
rette come differenza di quadrati si ottengono le due rette:
b
y=± x
a
Queste rette sono i due asintoti
dell’iperbole. Man mano aumenta il valore
della x, la distanza tra un punto della curva e
l’asintoto diminuisce, ma non arrivano mai a
intersecarsi. La curva all’infinito si comporta
come una retta, essendo distante
dall’asintoto circa 0.
Nel caso in figura i fuochi sono sull’asse delle
x. =(±
F c ;O)
F e F sono i due fuochi e .
1 2 1,2
√ 2 2
+b
c= a b
Il Vertice è il punto dove l’iperbole interseca l’asse. Se i fuochi sono sull’asse delle x,
a
è il semiasse non traverso perchè l’iperbole non interseca l’asse delle y e è l’asse
traverso. 2 2
y x
− =1 a
Se i fuochi sono sull’asse delle y , l’iperbole è , è l’asse non traverso e
2 2
b a
b è l’asse traverso.
a=b
Se , l’iperbole è EQUILATERA.
2 2
x y 2 2 2
⇒
− =1 − =a
x y
2 2
a b
In questo caso gli asintoti diventano le bisettrici
degli assi:








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









