Palloni gonfiati

Sì, la mongolfiera appartiene alla famiglia dei palloni gonfiati. I quali sono riempiti con un gas più leggero dell'aria. Idrogeno (H₂ , molto infiammabile) ed elio (He, gas nobile e quindi non ossidabile) sono i più comuni gas storicamente usati per riempire i palloni aerostatici. In entrambi i casi si tratta di gas con peso molecolare inferiore a quello dell'aria. La mongolfiera, invece, contiene aria calda, riscaldata dai fumi di combustione del propano.

Come è noto, le variabili che definiscono le condizioni di un gas lontano dal suo punto critico sono ben rappresentate dall'equazione dei gas perfetti:

Dunque la densità risulta:

. Quindi la densità dipende dalla pressione, dalla temperatura e dal peso molecolare. La stessa equazione vale, ovviamente, anche per l'aria che riempie l'atmosfera.

Ecco quindi che idrogeno ed elio che hanno PM inferiore all'aria, hanno densità inferiore a quella dell'aria a pari p e T. Mentre nel caso della mongolfiera la densità dell'aria interna al pallone è inferiore a quella dall'aria ambiente, a parità di pressione, grazie alla temperatura (T) superiore.

Si tenga presente che nell'equazione dei gas la temperatura è in gradi Kelvin (°K = °C +273.15).

Se riempiamo un pallone con gas leggero o con aria calda, questo sale verso l'alto, grazie al principio di Archimede: un corpo immerso in un fluido riceve una spinta verso l'alto pari al peso del volume di fluido spostato dal corpo

Se la densità del corpo è inferiore a quella del fluido, allora il suo peso risulta inferiore alla spinta archimedea e quindi il corpo viene sollevato. E' questo il caso del pallone aerostatico, che può salire a quote elevate (chilometri).

In questo problema ci vogliamo limitare al caso della mongolfiera. E' evidente, dall'equazione sopra riportata, che quanto più grande è la temperatura dell'aria calda, tanto minore risulta la densità. Tuttavia esiste un limite tecnico alla temperatura, pari a 120°C. Al disopra si danneggerebbe l'involucro del pallone.

Osserviamo che a differenza dei palloni gonfiati dai gas leggeri, la mongolfiera non e sigillata. Essa è aperta all'estremità inferiore per permettere l'entrata dei gas caldi di combustione del propano. In questo modo la pressione all'interno della mongolfiera è sempre uguale a quella dell'aria circostante.

Assumiamo che il pilota della mongolfiera possa modificare a piacere la temperatura dell'aria calda, nel campo 100 - 120 °C, con sapienti manovre di accensione/spegnimento del bruciatore a propano. E' intuitivo che ad ogni temperatura dell'aria calda corrisponda una quota di equilibrio della mongolfiera. All'equilibrio la spinta archimedea eguaglia il peso della mongolfiera.

Desideriamo fare dei calcoli di equilibrio ma prima dobbiamo studiare le caratteristiche dell'atmosfera in quota. Sappiamo che salendo in quota la temperatura e la pressione dell'aria decrescono. In che modo avviene? A questo risponde il modello ISA (International Standard Atmosphere), molto usato in numerose applicazioni pratiche.

Secondo ISA la variazione di T, p, ρ dell'aria in funzione della quota z è il seguente:

Dove: T₀ = 288,15 °K , p₀ =101325 Pa sono le condizioni al suolo (z=0).

I parametri sono:

,

,

.

Qui R è la costante dell'aria, che è data dal rapporto tra la costante universale dei gas e il peso molecolare dell'aria. Si vede quindi che la T decresce con un gradiente costante di circa mezzo grado per chilometro, mentre la pressione e la densità decrescono con un andamento più complesso. Ovviamente ISA è un modello che fornisce una approssimazione, valida per stime. Temperatura e pressione al suolo, nella realtà possono essere diverse e questo influenza i profili in quota. Ai fini dei nostri calcoli assumiamo che valga ISA.

DOMANDA 1 (Statica)

Una mongolfiera di massa solida( involucro, gondola, passeggeri, attrezzature) pari a 800 kg è dotata di un pallone di volume

. Scrivere l'equazione di equilibrio ( Peso complessivo = Spinta Archimedea) e determinare la T di equilibrio dell'aria calda nel pallone, in funzione della quota, alle seguenti quote: z = 0, 1000, 2000, 3000, 4000, 5000 m. Per far questo utilizzare il modello atmosferico ISA. (N.B. Il peso complessivo include la massa solida + la massa dell'aria calda contenuta nel pallone).

DOMANDA 2 (Dinamica)

Scrivere l'equazione di moto della mongolfiera (di massa solida e volume come da Domanda 1) che parte dal suolo. E calcolare il suo moto ascensionale. Trascurando l'effetto dei venti abbiamo un problema monodimensionale. Le forze da considerare la considerare sono: il peso complessivo, la spinta archimedea e la resistenza dell'aria al moto. Quest'ultima è espressa dalla nota formula:

.

A tal fine si consideri la mongolfiera assimilata ad una sfera di volume V. La variabile S è la sezione trasversale della sfera. Mentre u è la velocità verticale.

Anche per questa domanda utilizzare il modello ISA per quantificare le caratteristiche dell'aria in funzione della quota. Si tenga presente che la forma ben nota del secondo principio:

non è applicabile in questo caso, perché la massa complessiva è variabile.

Occorre dunque usare la forma generalizzata:

dove q è la quantità di moto:

.

Assumere che la durata dell'ascensione sia 15 minuti e che il pilota adotti una rampa di T, con estremi 100 °C e 120°C della durata di 10 minuti. Considerare

.

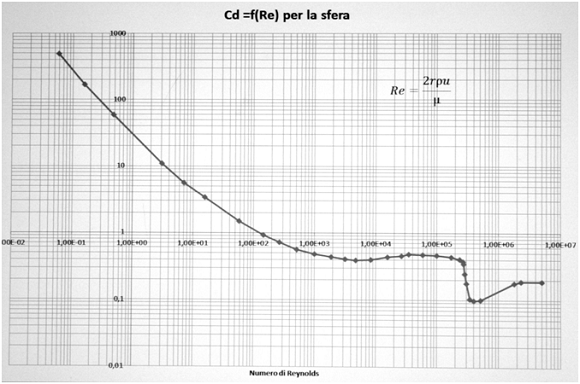
Nota: per informazione sotto viene riportato il diagramma del coefficiente di resistenza della sfera in funzione del numero di Reynolds.

LE SOLUZIONI DEL PROBLEMA

Mongolfiera statica
File Excel con la soluzione del caso statico

Mongolfiera dinamica
File Excel con la soluzione del caso dinamico