Funzioni - Fratte, irrazionali e grafici

Date due variabili x e y, si dice che y è funzione della variabile x se fra le due variabili esiste una relazione che ad ogni valore della x, appratenente ad un insieme D (dominio), fa corrispondere un solo valore per la y. Questo si esprime con la scrittura:
Y = f(x)
Ad esempio: y = 2x + 5
per x = 5 y = 10+5 = 15

Il valore di y dipende dal valore attribuioto alla x; per questo si dice che x è la variabile indipendente e y è la variabile dipendete.
L'insieme dei valori che si possono attribuire alla x (var.

Funzione razione fratta
Quando al secondo membro figura un polinomio che contiene operazioni sempre eseguibili per cui il campo di esistenza è (per ogni x appartenente a R.
Quando al secondo membro figura una frazione che sia la numeratore che al denominatore presenta dei polinomi per cui il campo di esistenza è dato da tutti i valori che possiamo attribuire alla x tranne quelli che annullano il denominatore.

Funzioni irrazionali
Quando la variabile indipendente figura sotto radice ora, se l'indice di radice è pari il radicando deve essere positivo o nullo (poiché non esiste la radice quadrata di un numero negativo) per cui il campo di esistenza si otterrà ponendo il radicando >(uguale) 0;
invece se l'indice di radice è dispari il radicando può essere anche negativo ed il campo di esistenza si riduce al dominio della funzione senza radice.

Rappresentazione grafica di una funzione
Si assegnano alla variabile indipendente x dei valori appratenenti al suo dominio e si ottengono i corrispondenti valori della y. A ciascuna coppia si associa il punto del piano cartesiano che ha come ascissa x e come ordinata y. Congiungendo tutti i punti si ottiene il grafico della nostra funzione.

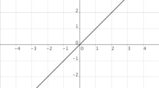
Funzione della proporzionalità diretta
Una funzione si dice di proporzionalità diretta se al variare di una variabile, varia proporzionalmente l'altra variabile. Ad esempio y=kx, dove y è la variabile dipendente, k è la costante (un numero) ed x la variabile indipendente. Quindi se una raddoppia l'altra raddoppia, se una quadruplica l'altra quadruplica e così via. Di conseguenza si può dire che il rapporto tra le due variabili dà un numero sempre uguale, una costante k.