Concetti Chiave
- Il Teorema del Valor Medio afferma che esiste almeno un punto nell'intervallo (a,b) in cui la tangente alla curva ha lo stesso coefficiente angolare della secante che unisce gli estremi.
- La funzione g(x) è continua sull'intervallo chiuso [a, b] e derivabile nei punti interni, condizione necessaria per applicare il teorema.
- Mathcad viene utilizzato per impostare un blocco risolutivo che aiuta a determinare il punto specifico c dove il teorema si verifica.
- L'animazione grafica illustra la relazione tra la secante e la tangente, facilitando la comprensione del teorema.
- Il contenuto sottolinea l'importanza del coefficiente angolare sia della tangente che della secante nell'analisi del Teorema del Valor Medio.
Coefficiente angolare tangente in
Coefficiente angolare secante :
Estremi dell'intervallo [a,b]
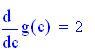
Coefficiente angolare tangente in
Coefficiente angolare secante :
Estremi dell'intervallo [a,b]
Per vedere l'animazione sul teorema del valor medio clicchiamo sul grafico seguente:
Rappresentazione grafica della secante g(t) congiungente gli estremi dell'intervallo [a,b] e della tangente in c.
In accordo con il Teorema del Valor Medio, esiste almeno un punto dell'intervallo (a,b) in cui il coefficiente angolare della retta tangente alla curva uguale a m a b . Impostiamo un blocco risolutivo di Mathcad per trovare tale punto:
Rapporto incrementale della funzione g(t) nell'intervallo [a,b]: 
Estremi dell'intervallo:
Funzione continua e derivabile in tutto R e quindi anche su [a,b]:
Sia y = g(x) un funzione continua sull'intervallo chiuso [a, b] e derivabile almeno nei punti interni ad esso, in tale ipotesi esiste almeno un punto c appartenente all'ntervallo aperto (a,b) tale che si abbia:
Il Teorema del Valor Medio animato con Mathcad (Carlo Elce)
Per vedere l'animazione sul teorema del valor medio clicchiamo sul grafico seguente:
Rappresentazione grafica della secante g(t) congiungente gli estremi dell'intervallo [a,b] e della tangente in c.
In accordo con il Teorema del Valor Medio, esiste almeno un punto dell'intervallo (a,b) in cui il coefficiente angolare della retta tangente alla curva uguale a m a b . Impostiamo un blocco risolutivo di Mathcad per trovare tale punto:
Rapporto incrementale della funzione g(t) nell'intervallo [a,b]:
Estremi dell'intervallo:
Funzione continua e derivabile in tutto R e quindi anche su [a,b]:
Sia y = g(x) un funzione continua sull'intervallo chiuso [a, b] e derivabile almeno nei punti interni ad esso, in tale ipotesi esiste almeno un punto c appartenente all'ntervallo aperto (a,b) tale che si abbia:
Il Teorema del Valor Medio animato con Mathcad (Carlo Elce)
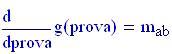
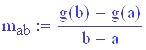
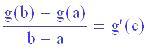
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
